ICC Crypto Challenges 2025

apia

Source code:

#!/usr/bin/env python3
 
from Crypto.Util.number import *
import os
 
with open("flag.txt", "rb") as f:
    FLAG = f.read()
FLAG += os.urandom(512 * 3 // 8 - 1 - len(FLAG))
 
p = getPrime(512)
q = getPrime(512)
N = p ** 2 * q
d = pow(N, -1, (p - 1) * (q - 1))
 
def encrypt(pt):
    return pow(pt, N, N)
 
def decrypt(ct):
    return pow(ct, d, p * q)
 
print("N:", N)
print("encrypted flag:", pow(bytes_to_long(FLAG), 0x10001, N))
 
# for test
while True:
    pt = int(input("plaintext: "))
    assert pt > 0
    print(decrypt(encrypt(pt)) == pt)

Phân tích:
Bài trên cho ta một hệ mã trông khá giống với hệ mã RSA. Với $N=p^{2}q$ và $d=N^{-1}\mathrm{mod}(p-1)(q-1)$
Hàm mã hóa:

$$m^N\mathrm{mod}N$$

Hàm giải mã:

$$c^d\mathrm{mod}pq$$

Bài cho ta một oracle để kiểm tra xem input ta nhập vào có thỏa mãn $Dec(Enc(m))=m$ hay không.
Đầu tiên thì mình cần hiểu cái công thức nó hoạt động như thế nào và khi nào oracle sẽ trả về True hoặc False. Sẽ có một số giá trị mà tại đó oracle sẽ trả về False:

Nếu $m=pq$ thì khi đó

$$Dec(Enc(m))=(m^N\mathrm{mod}N{)}^d\mathrm{mod}pq$$

Dẫn tới $m^N=(pq{)}^N\mathrm{mod}N=0$ cho nên $0^d\mathrm{mod}pq=0$ và nếu ta gửi đúng $m=pq$ tới server thì oracle sẽ trả về False.
Còn nếu như $m<pq$ thì sao? Lúc này ta đặt $m=pq-k$ với $k\in {\mathbb{Z}}^{\ast }$. Thì ta có

$$((pq-k{)}^N\mathrm{mod}N{)}^d\equiv ((pq-k{)}^N{)}^d\mathrm{mod}p$$

Tương tự với mod $q$. Cho nên nếu như $m<pq$ thì khi Decrypt ta sẽ lấy theo modulo $pq$ và oracle sẽ trả về True. Ngược lại nó sẽ trả về False nếu như $m=pq$ hoặc $m>pq$.
Từ giả thiết này ta có thể áp dụng tìm kiếm nhị phân để tìm ra $pq$ và khôi phục lại flag.

Solve script:

from pwn import *
from Crypto.Util.number import *
from sage.all import gcd
r = process(['python3', "chall.py"])
context.log_level = "debug"
r.recvuntil(b'N: ')
N = int(r.recvline().strip())
print(N)
r.recvuntil(b'encrypted flag: ')
enc_flag = int(r.recvline().strip())
print(enc_flag)
def query(x):
    r.sendlineafter(b'plaintext: ', str(x).encode())
    resp = r.recvline().decode()
    if resp == "True\n":
        return True
    else:
        return False 
 
left = 1 
right = N//2
modulus = 0 
while left <= right: 
    mid = (left+right)//2
    ans = query(mid)
    if ans:
        left = mid + 1 
    if not query(mid):
        right = mid  - 1 
modulus = left 
print(modulus)
p = N//modulus
q = modulus//p
d = pow(0x10001,-1,(q-1)*p*(p-1))
flag = long_to_bytes(pow(enc_flag,d,N))
print(flag)

SignCouple

Source code của bài:

#!/usr/bin/env python3
 
from gmpy2 import is_prime
import json
from random import SystemRandom
 
with open("flag.txt", "r") as f:
    FLAG = f.read()
 
random = SystemRandom()
 
def send(sender, receiver, data):
    print(f"{sender} -> {receiver}: {json.dumps(data)}")
    data = json.loads(input("mitm: "))
    return data
 
def getPrime(nbits):
    while True:
        p = random.randrange(2 ** (nbits - 1), 2 ** nbits) | 1
        if is_prime(p):
            return p
    
n = getPrime(1000)
print("n =", n)
 
e = 65537
nbits = 1024
 
class Alice:
    def __init__(self, secret_A):
        self.secret_A = secret_A
        self.share_A = 0
 
    def ot_setup(self):
        while True:
            p = getPrime(nbits // 2)
            q = getPrime(nbits // 2)
            self.N = p * q
            if (p - 1) * (q - 1) % e != 0:
                break
        self.d_ot = pow(e, -1, (p - 1) * (q - 1))
        self.x = [random.randrange(self.N), random.randrange(self.N)]
        data = {"N": self.N, "x": self.x}
        return send("Alice", "Bob", data)
 
    def ot_send_encrypted_messages(self, data, bit):
        secret = 2**bit * self.secret_A % n
 
        share = random.randrange(n)
        self.share_A += share
        self.share_A %= n
        m = [(-share) % n, (-share + secret) % n]
 
        v = data["v"]
        k = [pow(v - self.x[i], self.d_ot, self.N) for i in range(2)]
        data = {"enc_m": [(m[i] + k[i]) % self.N for i in range(2)]}
        return send("Alice", "Bob", data)
 
class Bob:
    def __init__(self, secret_B):
        self.secret_B = secret_B
        self.share_B = 0
 
    def ot_send_v(self, data, bit):
        self.N = data["N"]
        assert nbits - 1 <= self.N.bit_length() <= nbits
 
        self.b = (self.secret_B >> bit) & 1
        self.k = random.randrange(self.N)
        v = (data["x"][self.b] + pow(self.k, e, self.N)) % self.N
        data = {"v": v}
        return send("Bob", "Alice", data)
    
    def ot_decrypt_message(self, data):
        self.share_B += (data["enc_m"][self.b] - self.k) % self.N
        self.share_B %= n
 
class MtA:
    def __init__(self, alice, bob):
        self.alice = alice
        self.bob = bob
 
    def mul(self):
        for bit in range(1000):
            res = self.alice.ot_setup()
            res = self.bob.ot_send_v(res, bit)
            res = self.alice.ot_send_encrypted_messages(res, bit)
            self.bob.ot_decrypt_message(res)
 
alice = Alice(random.randrange(n))
bob = Bob(random.randrange(n))
 
mta = MtA(alice, bob)
mta.mul()
 
secret = mta.alice.secret_A * mta.bob.secret_B % n
guess = int(input(f"guess: "))
if guess == secret:
    print(FLAG)

Phân tích:
Bài có 2 class chính là class Alice và Bob.
Với class Alice: Đầu tiên nó sinh ra các bộ số $N,e,p,q$ rồi sau đó tính $d=e^{-1}\mathrm{mod}(p-1)(q-1)$. Data được tạo sẽ gồm modulus $N$ và cặp giá trị $x[0],x[1]$ được sinh ngẫu nhiên.
Đây là bước setup.
Tiếp theo là hàm send bao gồm các bước như sau:

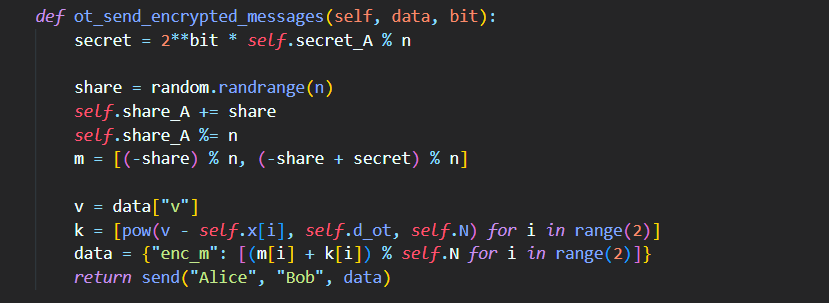
• Khởi tạo một giá trị secret $s=2^{bit}\times s_A\mathrm{mod}n$, $s_A$ ở đây là secret key của Alice
• Giá trị share $s^{\prime }$ sẽ được sinh ngẫu nhiên trong khoảng $[0,n)$.
• Sau đó $s_A=s_A+s^{\prime }\mathrm{mod}n$
• $m=[(-s^{\prime })\mathrm{mod}n,(-s^{\prime })+s\mathrm{mod}n]$
• $k=[(v-x[i]{)}^d\mathrm{mod}N,i=1,2]$
• Data lúc này sẽ là $[(m[i]+k[i])\mathrm{mod}N,i=1,2]$
  Nhìn chung thì khá là rắc rối :v

Sau đó thì ta có class Bob.
Ở trên ta có giá trị $v$, thì giá trị $v$ này sẽ được sinh ra bởi Bob và gửi tới cho Alice.

• $b=(s_B\gg bit)\&1$
• $k\in [0,N)$
• $v=(x[b]+k^e\mathrm{mod}N)\mathrm{mod}N$
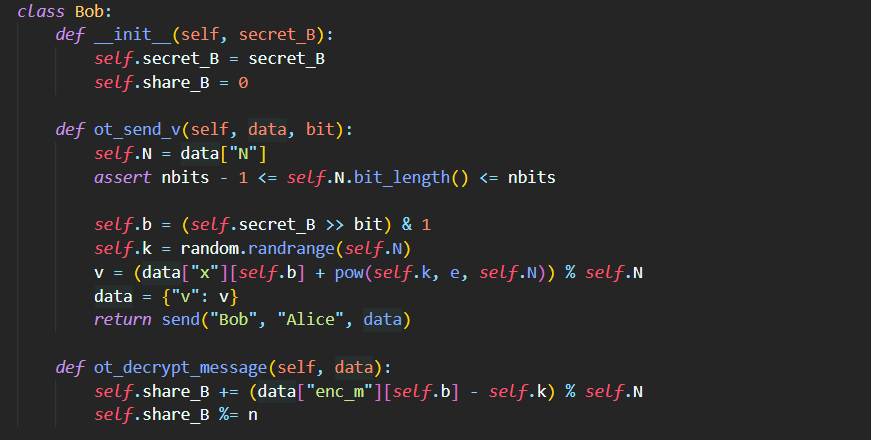
  Và gửi $v$ tới cho Alice
  Về phần giải mã:

$$s_B=(c[b]-k)\mathrm{mod}N$$

Tóm lại thì luồng của bài này sẽ như sau:
Đầu tiên, khởi tạo 2 giá trị secret A và secret B

alice = Alice(random.randrange(n))
bob = Bob(random.randrange(n))

Ta đặt là $s_A$ và $s_B$.
Sau đó chương trình sẽ gọi

mta = MtA(alice, bob)
mta.mul()

Hàm mul sẽ lặp 1000 lần

    def mul(self):
        for bit in range(1000):
            res = self.alice.ot_setup()
            res = self.bob.ot_send_v(res, bit)
            res = self.alice.ot_send_encrypted_messages(res, bit)
            self.bob.ot_decrypt_message(res)

Mỗi lần khi hàm send() được gọi thì ta sẽ được mitm, tức là thay đổi data đầu vào theo ý muốn của ta.
Mỗi vòng nó sẽ làm những việc sau:

• Gọi alice.ot_setup(). Hàm này như ta phân tích ở trên thì sẽ trả về send("Alice", "Bob", data)
  Data lúc này sẽ là $[x_1,x_2]$ với $i=1,2$. Các tham số mà Alice sinh ra sẽ bao gồm một modulus $N_a$ 1024 bit, số mũ bí mật $d_{ot}$ , các giá trị $x_1,x_2$ sẽ là ngẫu nhiên. Ta được can thiệp vào bước này để thay đổi giá trị của $N_a$ và cặp giá trị $x_1,x_2$.
• Sau bước này thì sẽ tới bước của Bob. Bob sẽ nhận data từ Alice ở bước trước đó cùng với đầu vào là bit của round này. Sau đó Bob tính $b$, chính là bit thứ $i$ của secret key $s_B$. $i$ chính là số round hiện tại (chính là bit trong vòng lặp kia).
  Sau đó sẽ chọn một giá trị $k$ random và gửi $(x[i]+k^e)\mathrm{mod}{N}_b$
  Bob chỉ gửi cho ta giá trị của $v$ còn $N_b$ thì sẽ được giấu.
• Bước thứ ba là của Alice. Khi alice nhận được $v$ thì Bob nó sẽ tiến hành mã hóa như sau: Tính secret, ta gọi là $s_{enc}$ chẳng hạn, bởi $s_{enc}=2^{bit}+s_A\mathrm{mod}n$ . Đây là nơi mà giá trị của $n$ đầu bài được sử dụng. Sau đó một số bí mật $s$ được sinh ngẫu nhiên. Ta có thể kí hiệu $s_i$ với $i$ là số vòng hiện tại cho thuận tiện. Và ta tính $s_A=s_A+s_i\mathrm{mod}n$. Cặp plaintext lúc này là $m=[(-s_i)\mathrm{mod}n,(-s_i+s_{enc})\mathrm{mod}n]$ , tất cả lấy theo modulo $n$ chứ không phải modulus $N_a,N_b$.
  Sau đó ta có $k[i]=(v-x[i]{)}^d\mathrm{mod}N$ với mỗi $i$ và ciphertext $c[i]=m[i]+k[i]$. Ta sẽ gửi ciphertext này cho Bob, ở bước này ta cũng có thể thực hiện mitm được
  Bit của round được dùng để tính $s_{e}nc$
  Cuối cùng:
• Bob nhận $c[]$ và giải mã bằng cách lấy $c[i]-k_b$ và cộng dồng lại vào $s_B$. Giá trị này không bao giờ được in ra nên ta cũng không biết nó là bao nhiêu.
  Để lấy được flag thì ta cần đoán được giá trị của secret là bao nhiêu sau 1000 vòng:

secret = mta.alice.secret_A * mta.bob.secret_B % n
guess = int(input(f"guess: "))
if guess == secret:
    print(FLAG)

Để làm được như vậy thì ta phải track được giá trị của $s_A$ và $s_B$ sau mỗi vòng.

Secret key của $B$ bị lộ khi nào? Nó sẽ bị lộ duy nhất ở bước thứ hai là bước send_v. Một bit của $v$ sẽ bị tiết lộ thông qua $v$. Nó sẽ chọn 1 trong 2 messages từ data mà $A$ gửi tới, tức là cặp $x_1,x_2$. Vậy ta sẽ cần chọn $N_A,x_1,x_2$ sao cho sau khi nhận lại $v$ thì ta biết được ngay đó là $x_1$ hay $x_2$.
Ý tưởng để recover lại như sau:
Đầu tiên ta chọn $N_A=p$ sao cho $e|p-1$ còn cặp giá trị $x$ sẽ chọn $[0,1]$.
Bằng cách này khi ta gửi tới Bob giá trị $p,[0,1]$. Nó sẽ tính

$$x[i]+k^e\mathrm{mod}p$$

Vì $e$ là ước của $p-1$ nên ta có thể viết $p-1=te$. Như vậy

$$k^e=k^{(p-1)/t}\mathrm{mod}p$$

Nếu ta thử lấy $v-x[i]$ rồi mũ cho $t$, ở đây ta biết giá trị của $t$, và thu được kết quả là $1$. Thì chứng tỏ, $x[i]$ mà ta chọn là đúng.
Vì $k^{p-1}=1\mathrm{mod}p$
Đầu tiên là tìm $p,t$.

t = 1
while True: 
    p = t*e + 1 
    if is_prime(p):
        break 
    else:
        t+=1 
print(p)
print(t)
# 917519
# 14

Nhưng số này không đủ lớn do chương trình yêu cầu số $N$ của ta nhập vào phải thỏa

assert nbits - 1 <= self.N.bit_length() <= nbits

Tất nhiên việc brute tìm 1 số 1024 bits là điều bất khả thi rồi nên mình cần làm một cách tối ưu hơn.
Do $p$ mà ta sinh ra ở trên thỏa đồng dư 1 module $e$ nên cho dù lũy thừa lên bao nhiêu vẫn thỏa mãn phương trình đồng dư. Vậy ta chỉ cần mũ nó lên. Nhưng việc lấy mũ không cho ta một số đủ trong bit length đó nên ta cần sinh ra thêm 1 số khác mà có bit length thêm vào đủ để rơi vào trong range trên.
… Nhưng đáng tiếc là mình không làm được theo hướng này : D vì không có số nguyên tố nào thỏa cả?

Vì vậy thay vì tự sinh ra một số $p$ thì mình sẽ lợi dụng giá trị của $N_A$ để thêm thông tin của $p$ vào. Bằng cách lấy $N_A/p$ rồi nhân lại với $p$. Chia ở đây là chia lấy phần nguyên.

Tiếp theo là xử lí $s_A$.
Ta đang dừng lại ở bước gửi $v$.
Sercet key của $A$ sẽ bị leak ở bước nào? Ở 2 bước sau này thì các giá trị $s_A,s_B$ sẽ được cập nhật lại nên ta cũng cần track luôn cả phần giá trị được cộng thêm vào.
Nếu như ta khôi phục được cả hai giá trị $m_0,m_1$ thì sao? Ta sẽ khôi phục được $s_A\mathrm{mod}n$?
Ta cần chọn $v$ sao cho $(v-x_0{)}^d+(v-x_1{)}^d\mathrm{mod}{N}_A$ triệt tiêu để $m_0+m_1=s_A$. Ta sẽ chọn $v=(x_0+x_1)/2\mathrm{mod}{N}_A$ là được.
Nhưng ta cần cẩn thận vì đang làm việc với modulo $n$ lẫn $N_A$ nên cách này sẽ không hiệu quả. Mình có thử test thì rõ ràng kết quả là không giống nhau.
Vậy nên xử lí như thế nào?
Mình sẽ sử dụng ý tưởng đã từng được sử dụng trong bài DiceCTF 2025

Với secret key của alice là $s_A$, ta kí hiệu $s_i=2^i{s}_A$ trong đó $s_i$ là secret ở mỗi vòng mà ta cần recover.
Hai ciphertext của nó sẽ có dạng $c_0=t+(v-x_0{)}^d\mathrm{mod}{N}_A$ và $c_1=((t+s_i)\mathrm{mod}n)+(v-x_1{)}^d\mathrm{mod}{N}_A$ . Chọn $m\ge 2$ và chọn $v$ sao cho $\frac{v-x_1}{v-x_0}=m^e\mathrm{mod}{N}_A$ để sau khi Alice tính xong $k$ thì ta được

$$\begin{array}{l}{c}_1-m{c}_0=((t+s_i)\mathrm{mod}n)-mt\mathrm{mod}{N}_A\end{array}$$

Đến đây sẽ có 2 trường hợp.
Trường hợp 1 là $(t+s_i)\mathrm{mod}n=(t+s_i)$ hoặc là $t+s_i-n$. Vì $t\in [0,n)$ còn $s_i\in [0,n)$ vì được lấy modulo $n$. Cho nên $t+s_i\in [0,2n-2)$ dẫn tới 1 trong 2 trường hợp ở trên.
Như vậy khi tách ra cũng sẽ có 2 trường hợp cho $(c_1-m{c}_0)\mathrm{mod}{N}_A$ đó là $s_i\mathrm{mod}n-(m-1)t+N$hoặc là $s_i\mathrm{mod}n-(m-1)t-n+N$.
Nhưng nếu chỉ có mỗi $s_i$ thì ta không thể recover lại được secret của alice mà cần xét thêm $s_{i+1}$ nữa. Cụ thể ta lấy

$$s_{i+1}=2s_i\mathrm{mod}n$$

… cập nhật sau

from pwn import *
from Crypto.Util.number import isPrime
import json
from tqdm import tqdm
 
context.log_level = "info"
r = process(["python3", "chall.py"])
 
r.recvuntil(b"n = ")
n = int(r.recvline().strip())
print(n)
 
e = 65537
nbits = 1024
 
p1 = 917519
assert (p1 - 1) % e == 0
exp_e_power = (p1 - 1) // e
 
bob_secret = 0
q_candidates = [0]
mod = 2**20
w0 = 1
w1 = mod + 1
 
for bit in tqdm(range(1000)):
    r.recvuntil(b"Alice -> Bob: ")
    line = r.recvline().strip().decode()
    data = json.loads(line)
 
    N_A = data["N"]
    x = data["x"]
 
    N_mitm = (N_A // p1) * p1
    assert nbits - 1 <= N_mitm.bit_length() <= nbits
 
    forged = {"N": int(N_mitm), "x": x}
    r.sendline(json.dumps(forged).encode())
 
    r.recvuntil(b"Bob -> Alice: ")
    line = r.recvline().strip().decode()
    data = json.loads(line)
    v_from_bob = data["v"]
 
    b_bit = 0
    if pow(v_from_bob - x[1], exp_e_power, p1) == 1:
        b_bit = 1
    bob_secret |= (b_bit << bit)
 
    c0 = pow(w0, e, N_A)
    c1 = pow(w1, e, N_A)
    inv = pow((c0 - c1) % N_A, -1, N_A)
    v_tampered = (inv * (c0 * x[1] - c1 * x[0])) % N_A
 
    data_to_alice = {"v": int(v_tampered)}
    r.sendline(json.dumps(data_to_alice).encode())
 
    r.recvuntil(b"Alice -> Bob: ")
    line = r.recvline().strip().decode()
    data = json.loads(line)
    enc_m = data["enc_m"]
    enc0, enc1 = enc_m[0], enc_m[1]
 
    y = (enc1 * w0 - enc0 * w1) % N_A
    y -= N_A
    y %= mod
 
    if bit == 0:
        y0 = y
    else:
        new_candidates = []
        two_bit_mod = pow(2, bit, mod)
        for q in q_candidates:
            for q1 in (2 * q, 2 * q + 1):
                if (
                    y == (two_bit_mod * y0 - q1 * n) % mod or
                    y == (two_bit_mod * y0 - (q1 + 1) * n) % mod or
                    y == (two_bit_mod * (y0 + n) - q1 * n) % mod or
                    y == (two_bit_mod * (y0 + n) - (q1 + 1) * n) % mod
                ):
                    new_candidates.append(q1)
        q_candidates = list(set(new_candidates))
        log.info(f"bit {bit}: {len(q_candidates)} candidates")
 
    r.sendline(json.dumps(data).encode())
 
q_last = q_candidates[0]
alice_secret = (q_last * n + 2**999 - 1) // (2**999)
 
for delta in range(10):
    cand = alice_secret + delta
    if cand % mod == y0 or (cand - n) % mod == y0:
        alice_secret = cand
        break
 
secret = (alice_secret * bob_secret) % n
r.sendline(str(secret).encode())
r.interactive()