Block Cipher Review

Nhắc lại một số thứ

AES-128

Trước tiên ta xem lại cách mà AES hoạt động. Phiên bản AES mà mình phân tích sẽ là AES-128 bit.
Tài liệu chính thức cho tiêu chuẩn mã hóa AES: https://nvlpubs.nist.gov/nistpubs/fips/nist.fips.197.pdf

Vì AES-128 thực hiện mã khóa trên từng khối có độ lớn 16 bytes cho nên ta sẽ biểu diễn plaintext bằng cách ánh xạ các kí tự sang một ma trận có kích thước là $4\times 4$. Một ma trận như vậy sẽ được gọi là ma trận trạng thái.

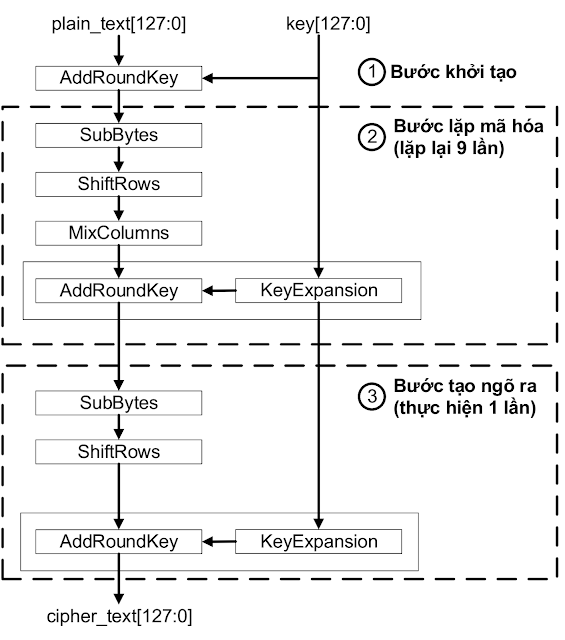
Tiếp theo ta có sơ đồ cho thuật toán như dưới đây:

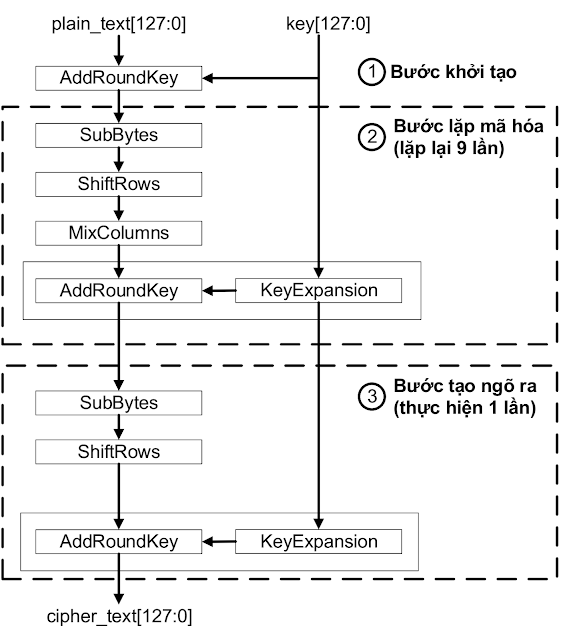
Bước 1. Bước đầu tiên sẽ là add round key.
Ở bước này ta sẽ XOR từng phần tử của ma trận trạng thái với từng phần tử của round key. Round key ở đây là đầu ra của một bước gọi là KeyExpand. Ta sẽ bàn về bước này sau.

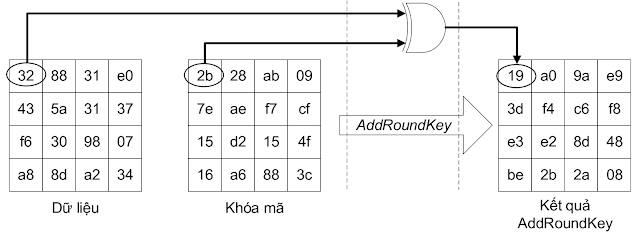
Sau khi kết thúc phép XOR thì ta thu được một ma trận kết quả mới làm đầu vào cho bước tiếp theo.

Bước 2. SubBytes
Ở bước này ta sẽ thay thế từng phần tử trong ma trận trạng thái bằng một phần tử khác trong một bảng gọi là SBox


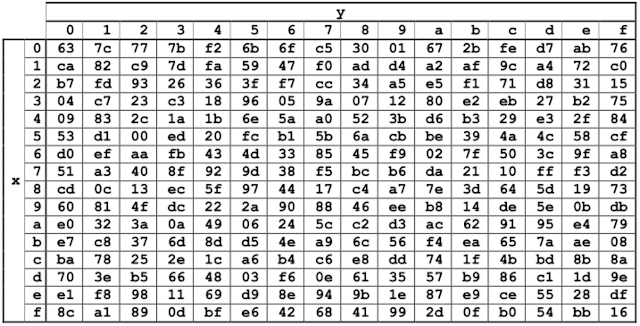
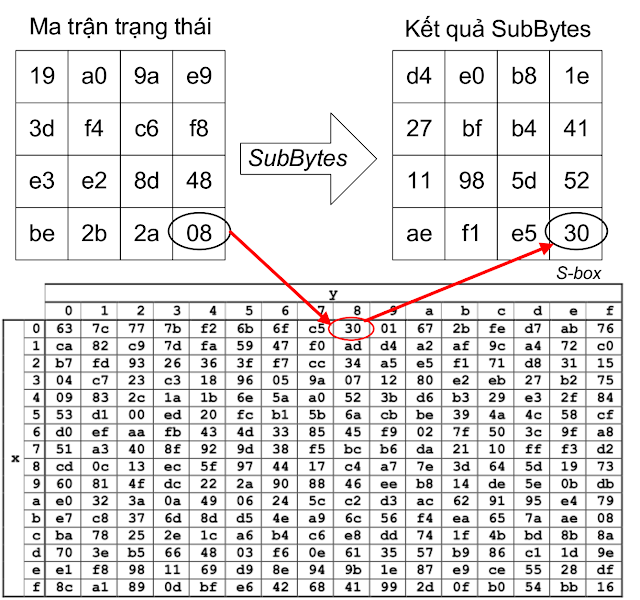
Bảng này đảm bảo mỗi byte sẽ được ánh xạ tới 1 byte duy nhất (song ánh). Cho nên ta có thể tạo một bảng tra cứu ngược để khôi phục lại ma trận trạng thái.

Bước 3. ShiftRows
Chức năng ShiftRows thực hiện quay trái từng hàng của ma trận trạng thái, ngõ ra của SubBytes, theo byte với hệ số quay tăng dần từ 0 đến 3. Hàng đầu tiên có hệ số quay là 0 thì các byte được giữ nguyên vị trí. Hàng thứ hai có hệ số quay là 1 thì các byte được quay một byte. Hàng thứ ba quay hai byte và hàng thứ tư quay ba byte.

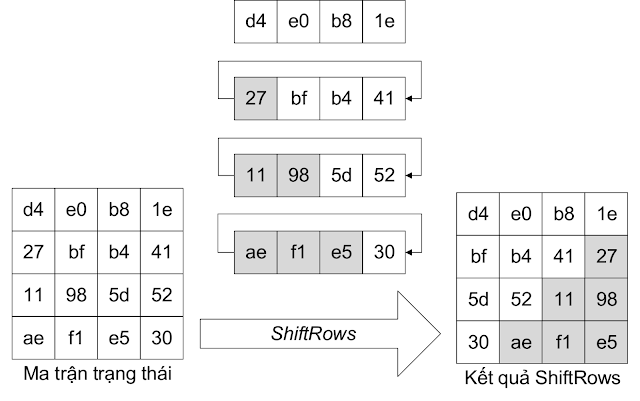
Bước 4. MixColumns
Chức năng MixColumns thực hiện nhân từng cột của ma trận trạng thái, ngõ ra của ShiftRows, với một ma trận chuyển đổi được quy định bởi chuẩn AES.

Việc biến đổi mỗi cột của ma trận trạng thái được thực hiện bởi hai phép toán là $\times$ và $\oplus$

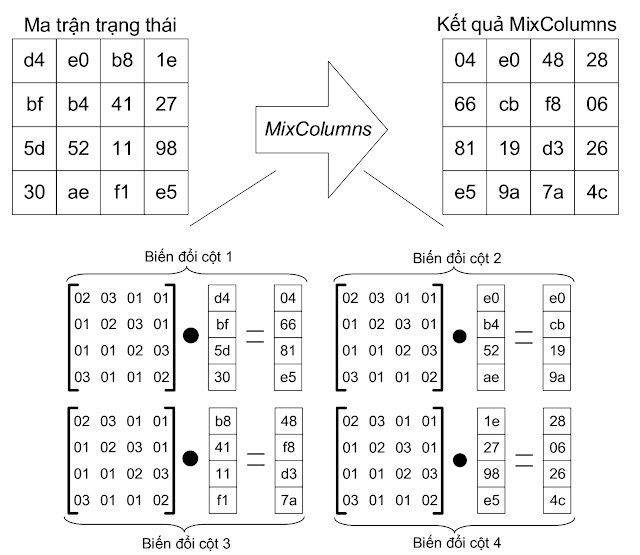
Toàn bộ Implement như sau:

N_ROUNDS = 10
 
def bytes_to_matrix(text: bytes):
    assert len(text) == 16
    return [[text[4*c + r] for r in range(4)] for c in range(4)]
 
def matrix_to_bytes(matrix):
    out = []
    for c in range(4):
        for r in range(4):
            out.append(matrix[c][r])
    return bytes(out)
 
def add_round_key(s,k):
    assert len(s) == len(k)
    for i in range(len(s)):
        for j in range(len(s)):
            s[i][j]^=k[i][j]
    
s_box = (
    0x63, 0x7C, 0x77, 0x7B, 0xF2, 0x6B, 0x6F, 0xC5, 0x30, 0x01, 0x67, 0x2B, 0xFE, 0xD7, 0xAB, 0x76,
    0xCA, 0x82, 0xC9, 0x7D, 0xFA, 0x59, 0x47, 0xF0, 0xAD, 0xD4, 0xA2, 0xAF, 0x9C, 0xA4, 0x72, 0xC0,
    0xB7, 0xFD, 0x93, 0x26, 0x36, 0x3F, 0xF7, 0xCC, 0x34, 0xA5, 0xE5, 0xF1, 0x71, 0xD8, 0x31, 0x15,
    0x04, 0xC7, 0x23, 0xC3, 0x18, 0x96, 0x05, 0x9A, 0x07, 0x12, 0x80, 0xE2, 0xEB, 0x27, 0xB2, 0x75,
    0x09, 0x83, 0x2C, 0x1A, 0x1B, 0x6E, 0x5A, 0xA0, 0x52, 0x3B, 0xD6, 0xB3, 0x29, 0xE3, 0x2F, 0x84,
    0x53, 0xD1, 0x00, 0xED, 0x20, 0xFC, 0xB1, 0x5B, 0x6A, 0xCB, 0xBE, 0x39, 0x4A, 0x4C, 0x58, 0xCF,
    0xD0, 0xEF, 0xAA, 0xFB, 0x43, 0x4D, 0x33, 0x85, 0x45, 0xF9, 0x02, 0x7F, 0x50, 0x3C, 0x9F, 0xA8,
    0x51, 0xA3, 0x40, 0x8F, 0x92, 0x9D, 0x38, 0xF5, 0xBC, 0xB6, 0xDA, 0x21, 0x10, 0xFF, 0xF3, 0xD2,
    0xCD, 0x0C, 0x13, 0xEC, 0x5F, 0x97, 0x44, 0x17, 0xC4, 0xA7, 0x7E, 0x3D, 0x64, 0x5D, 0x19, 0x73,
    0x60, 0x81, 0x4F, 0xDC, 0x22, 0x2A, 0x90, 0x88, 0x46, 0xEE, 0xB8, 0x14, 0xDE, 0x5E, 0x0B, 0xDB,
    0xE0, 0x32, 0x3A, 0x0A, 0x49, 0x06, 0x24, 0x5C, 0xC2, 0xD3, 0xAC, 0x62, 0x91, 0x95, 0xE4, 0x79,
    0xE7, 0xC8, 0x37, 0x6D, 0x8D, 0xD5, 0x4E, 0xA9, 0x6C, 0x56, 0xF4, 0xEA, 0x65, 0x7A, 0xAE, 0x08,
    0xBA, 0x78, 0x25, 0x2E, 0x1C, 0xA6, 0xB4, 0xC6, 0xE8, 0xDD, 0x74, 0x1F, 0x4B, 0xBD, 0x8B, 0x8A,
    0x70, 0x3E, 0xB5, 0x66, 0x48, 0x03, 0xF6, 0x0E, 0x61, 0x35, 0x57, 0xB9, 0x86, 0xC1, 0x1D, 0x9E,
    0xE1, 0xF8, 0x98, 0x11, 0x69, 0xD9, 0x8E, 0x94, 0x9B, 0x1E, 0x87, 0xE9, 0xCE, 0x55, 0x28, 0xDF,
    0x8C, 0xA1, 0x89, 0x0D, 0xBF, 0xE6, 0x42, 0x68, 0x41, 0x99, 0x2D, 0x0F, 0xB0, 0x54, 0xBB, 0x16,
)
inv_sbox = [0] * 256
for idx, val in enumerate(s_box):
    inv_sbox[val] = idx 
def sub_bytes(s):
    for i in range(len(s)):
        for j in range(len(s)):
            s[i][j] = s_box[s[i][j]]
 
def inv_sub_bytes(s):
    for i in range(4):
        for j in range(4):
            s[i][j] = inv_sbox[s[i][j]]
 
def shift_rows(s):
    s[0][1], s[1][1], s[2][1], s[3][1] = s[1][1], s[2][1], s[3][1], s[0][1]
    s[0][2], s[1][2], s[2][2], s[3][2] = s[2][2], s[3][2], s[0][2], s[1][2]
    s[0][3], s[1][3], s[2][3], s[3][3] = s[3][3], s[0][3], s[1][3], s[2][3]
 
 
def inv_shift_rows(s):
    s[0][1], s[1][1], s[2][1], s[3][1] = s[3][1], s[0][1], s[1][1], s[2][1]
    s[0][2], s[1][2], s[2][2], s[3][2] = s[2][2], s[3][2], s[0][2], s[1][2]
    s[0][3], s[1][3], s[2][3], s[3][3] = s[1][3], s[2][3], s[3][3], s[0][3]
 
 
# learned from http://cs.ucsb.edu/~koc/cs178/projects/JT/aes.c
xtime = lambda a: (((a << 1) ^ 0x1B) & 0xFF) if (a & 0x80) else (a << 1)
 
 
def mix_single_column(a):
    # see Sec 4.1.2 in The Design of Rijndael
    t = a[0] ^ a[1] ^ a[2] ^ a[3]
    u = a[0]
    a[0] ^= t ^ xtime(a[0] ^ a[1])
    a[1] ^= t ^ xtime(a[1] ^ a[2])
    a[2] ^= t ^ xtime(a[2] ^ a[3])
    a[3] ^= t ^ xtime(a[3] ^ u)
 
 
def mix_columns(s):
    for i in range(4):
        mix_single_column(s[i])
 
 
def inv_mix_columns(s):
    # see Sec 4.1.3 in The Design of Rijndael
    for i in range(4):
        u = xtime(xtime(s[i][0] ^ s[i][2]))
        v = xtime(xtime(s[i][1] ^ s[i][3]))
        s[i][0] ^= u
        s[i][1] ^= v
        s[i][2] ^= u
        s[i][3] ^= v
 
    mix_columns(s)
def expand_key(master_key):
    r_con = (
        0x00, 0x01, 0x02, 0x04, 0x08, 0x10, 0x20, 0x40,
        0x80, 0x1B, 0x36, 0x6C, 0xD8, 0xAB, 0x4D, 0x9A,
        0x2F, 0x5E, 0xBC, 0x63, 0xC6, 0x97, 0x35, 0x6A,
        0xD4, 0xB3, 0x7D, 0xFA, 0xEF, 0xC5, 0x91, 0x39,
    )
 
    key_columns = bytes_to_matrix(master_key)
    iteration_size = len(master_key) // 4
    i = 1
    while len(key_columns) < (N_ROUNDS + 1) * 4:
        # Copy previous word.   
        word = list(key_columns[-1])
 
        # Perform schedule_core once every "row".
        if len(key_columns) % iteration_size == 0:
            # Circular shift.
            word.append(word.pop(0))
            # Map to S-BOX.
            word = [s_box[b] for b in word]
            # XOR with first byte of R-CON, since the others bytes of R-CON are 0.
            word[0] ^= r_con[i]
            i += 1
        elif len(master_key) == 32 and len(key_columns) % iteration_size == 4:
            # Run word through S-box in the fourth iteration when using a
            # 256-bit key.
            word = [s_box[b] for b in word]
 
        # XOR with equivalent word from previous iteration.
        word = bytes(i^j for i, j in zip(word, key_columns[-iteration_size]))
        key_columns.append(word)
 
    # Group key words in 4x4 byte matrices.
    return [key_columns[4*i : 4*(i+1)] for i in range(len(key_columns) // 4)]
 
def encrypt(key, plaintext):
    round_keys = expand_key(key)
    text = bytes_to_matrix(plaintext)
    add_round_key(text, round_keys[0])
    for i in range(1, N_ROUNDS):
        sub_bytes(text)
        shift_rows(text)
        mix_columns(text)
        add_round_key(text,round_keys[i])
    sub_bytes(text)
    shift_rows(text)
    add_round_key(text,round_keys[10])
    ciphertext = matrix_to_bytes(text)
    return ciphertext 
 
 
def decrypt(key, ciphertext):
    round_keys = expand_key(key) # Remember to start from the last round key and work backwards through them when decrypting
 
    # Convert ciphertext to state matrix
    text = bytes_to_matrix(ciphertext)
    # Initial add round key step
    add_round_key(text, round_keys[10])
 
    for i in range(N_ROUNDS - 1, 0, -1):
        inv_shift_rows(text)
        inv_sub_bytes(text)
        add_round_key(text, round_keys[i])
        inv_mix_columns(text)
    # Run final round (skips the InvMixColumns step)
    inv_shift_rows(text)
    inv_sub_bytes(text)
    add_round_key(text, round_keys[0])
    # Convert state matrix to plaintext
 
    plaintext = matrix_to_bytes(text)
    return plaintext
if __name__ == "__main__":
    import os 
    key = os.urandom(16)
    pt  = os.urandom(16)
    ct = encrypt(key, pt)
    pt_ = decrypt(key,ct) 
    assert pt == pt_
    print("Thuat toan chay on, plaintext ban dau la :" ,f"{pt}")

Bây giờ mình sẽ phân tích lại bước KeyExpansion:
Mục đích của bước này là tạo một lịch khóa (key schedule) nhằm sinh ra các khóa khác nhau từ khóa vòng. Lí do ta cần bước này là vì AES có tổng cộng 10 rounds, số khóa vòng là 10 tương ứng với 9 lần AddRoundKey ở bước lặp mã hóa và 1 lần AddRoundKey ở bước tạo ngõ ra. Cho nên để tăng tính ngẫu nhiên của thuật toán ta sẽ sử dụng mỗi khóa vòng khác nhau ở mỗi bước lặp.

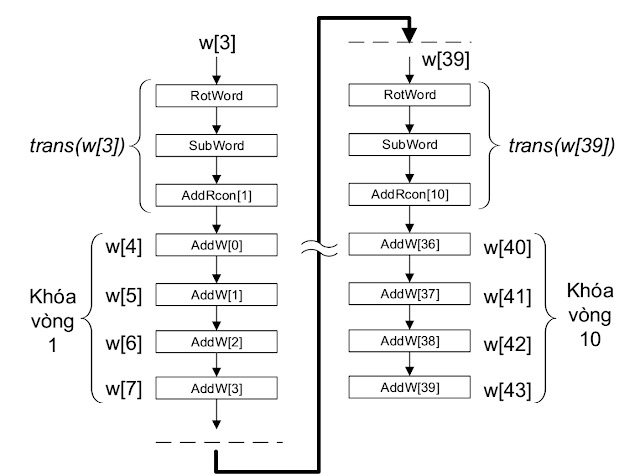
Chức năng KeyExpansion được thực hiện thông qua 4 bước chính là RotWord, SubWord, AddRcon và AddW. Nó sẽ nhận đầu vào là một khóa vòng 16 bytes và đầu ra là một danh sách gồm 44 từ (176 bytes).
Khóa vòng của ta ban đầu được chia làm 4 từ, mỗi từ 4 bytes, sau đó chuyển thành một ma trận $4\times 4$.
Pseudo code cho bước này:

RotWord là thực hiện quay trái một byte của từ

Bước SubWord là thay thế mỗi byte của từ thành một byte trong bảng SBox
Rcon là là các hằng số (round constant) cho mỗi vòng của KeyExpansion: Mọi người tham khảo tại đây: https://en.wikipedia.org/wiki/AES_key_schedule

DES

Lưu đồ thuật toán mã hóa DES như sau:

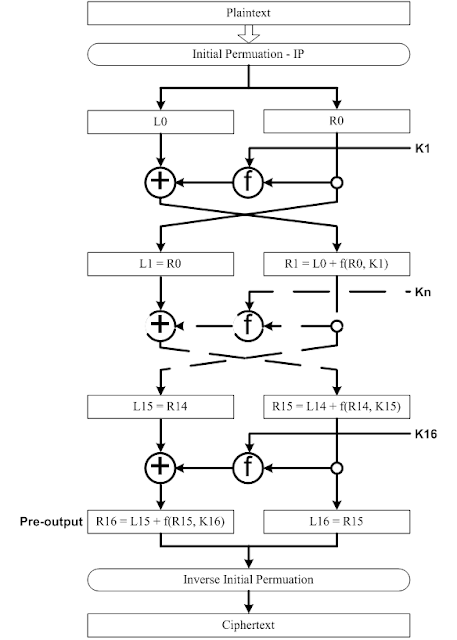
DES thực hiện tính toán dựa trên Key, thông qua một hàm $f$ , gọi là hàm mã khóa và một hàm được gọi là key schedule. Hàm này tạo ra các khóa vòng cho các lần lặp mã khóa. Có tổng cộng 16 vòng và do đó ta cần 16 khóa vòng.

Đầu tiên là bước hoán vị khởi tạo

Hoán vị khởi tạo

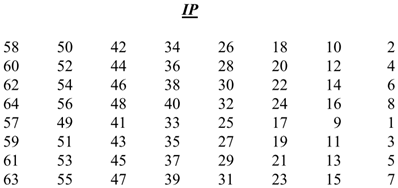
Hoán vị là thay đổi vị trí của các bit trong chuỗi giá trị nhưng không làm thay đổi giá trị của các bit này. Đầu vào của ta là một plaintext có độ lớn 64 bit. Sau đó được hoán vị theo bảng IP. Như trong hình thì bit thứ 58 của plaintext sẽ được dời lên đầu, còn bit thứ 7 thì dời về cuối.

Sau hoán vị, giá trị này sẽ được chia ra làm 2 nửa là $L_0$ và $R_0$. Đoạn $L_0$ bao gồm các bit từ vị trí 1 tới bit thứ 32, còn $R_0$ bao gồm các bit từ vị trí 33 tới 64.
Kế tiếp, các đoạn này sẽ được tính toán dựa vào công thức sau đây:

$$\begin{array}{l}{L}_{n+1}=R_n\\ R_{n+1}=L_n\oplus f(R_n,K_{n+1})\end{array}$$

Hàm $f(R,K)$:

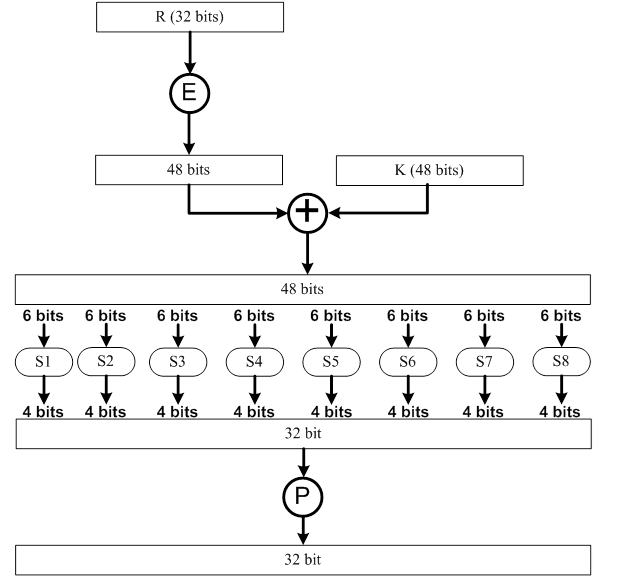
Đầu tiên, 32 bit của đoạn R sẽ được chuyển đổi thông qua bảng tra cứu E.

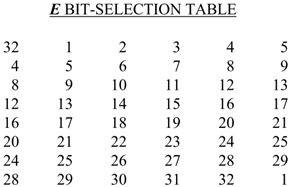
Trong bảng $E$ ta thấy có một số vị trí có giá trị được lặp lại. Ví dụ bit thứ 32 của $R$ sẽ được dời lên đầu, bit thứ nhất thì đặt vào vị trí thứ hai và vị trí cuối cùng của đầu ra.

Sau đó giá trị đầu ra 48 bits sẽ được XOR với key round cũng có độ dài 48 bits.

Kết quả phép XOR sau đó được chia thành 8 block và được đưa vào các hàm chuyển đổi $S_1,S_2,...,S_8$.

Việc chuyển đổi giá trị của các hàm này được thực hiện bằng cách tách block 6 bit thành hai phần. Phần thứ nhất là tổ hợp của bit đầu tiên và bit cuối cùng của block để tạo thành 2 bit chọn hàng của bảng S, bảng S có 4 hàng được đánh số từ 0 đến 3 theo thứ tự từ trên xuống. Phần thứ 2 là 4 bit còn lại dùng để chọn cột của bảng S, bảng S có 16 cột được đánh số từ 0 đến 15 theo thứ tự từ trái qua phải. Như vậy, với mỗi block 8 bit ta chọn được 1 giá trị trong bảng S. Giá trị này nằm trong khoảng từ 0 đến 15 sẽ được quy đổi thành chuỗi nhị phân 4 bit tương ứng. Các chuỗi nhị phân có được sau khi chuyển đổi từ S1 đến S8 sẽ được ghép lại theo thứ tự từ trái qua phải để tạo thành một giá trị 32 bit.

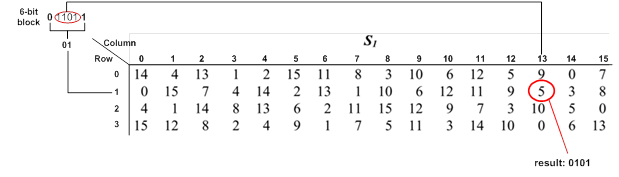
Cuối cùng, đầu ra 32 bits lại được tra cứu trong bảng hoán vị P trước khi được dùng cho bước tiếp theo là XOR với $L$.

Tính khóa vòng
Một key có 64 bit nhưng chỉ có 56 bit được sử dụng để thực hiện tính toán giá trị khóa vòng. Key được chia làm 8 byte. Các bit ở vị trí 8, 16, 32, 40, 48, 56 và 64 là các bit parity được sử dụng để kiểm tra độ chính xác của key theo từng byte vì khi key được phân phối trên đường truyền đến bộ mã hóa giải mã thì có thể xảy ra lỗi.

Như vậy trước khi tính khóa vòng, nó sẽ chọn bỏ đi 8 bit rồi mới bắt đầu tính.

Quy trình tính khóa vòng như sau:

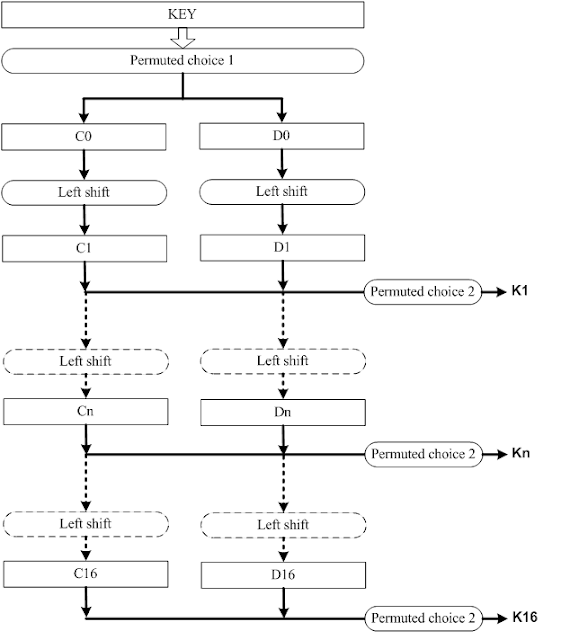
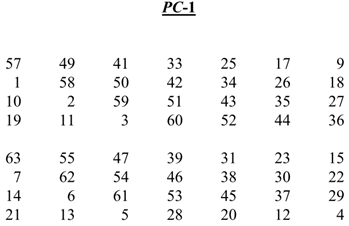
Bước đầu tiên, key sẽ được hoán vị dựa trên quy tắc trong bảng trên và lấy đầu ra là $C_0,D_0$.
Kể từ đây, các khóa vòng $K_n$ với $n$ từ 1 tới 16 sẽ được tính dựa vào công thức:

$$K_n=P{C}_2(C_n{D}_n)$$

Trong đó $C_n,D_n$ thu được từ $C_{n-1},D_{n-1}$ thông qua phép dịch trái (left shift). Số bit cần dịch được quy định thông qua bảng sau:

Sau khi dịch bit sau thì các bit sẽ được đánh số từ 1 tới 56 theo thứ tự trái sang phải và được lựa chọn lại thông qua bảng Permutation Choice 2

Bước cuối cùng trong giá trị mã hóa là hoán vị đảo $I{P}^{-1}$. Đầu ra của vòng thứ 16 sẽ một lần nữa được hoán vị và lấy kết quả làm ciphertext.

Các mode AES

Trên thực tế, các văn bản đầu vào thường có kích thước lớn kích thước của một block trong AES. Cho nên để thực hiện mã hóa và giải mã thì ta cần chia đầu vào thành các block khác nhau rồi xử lí chúng.

AES - ECB

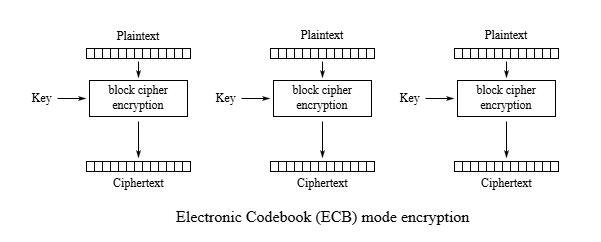
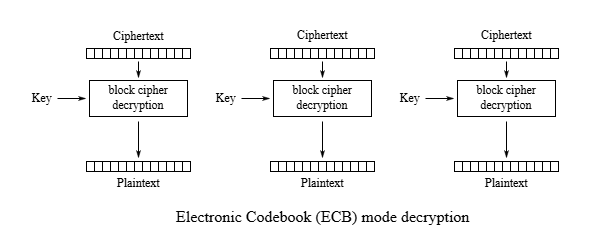
Mode ECB là mode đơn giản nhất trong số các mode của AES. Mode này thực hiện chia ciphertext thành các block rồi mã hóa độc lập từng block với nhau.
Điều này nảy sinh một vấn đề đó chính là: Các khối dữ liệu giống nhau thì kết quả mã hóa cũng sẽ tương tự nhau.

AES - GCM

Vấn đề với AES thông thường đó chính là nó không có cơ chế xác thực tin nhắn. Tức là kể cả khi ciphertext bị thay đổi thì oracle vẫn thực hiện giải mã hợp lệ.

Vì thế người ta quyết định thêm một kĩ thuật xác thực dùng khóa bí mật - MAC vào trong AES và từ đó ta có AES-GCM. GCM là viết tắt của Galois/Counter Mode và ta sẽ đi tìm hiểu từng phần của nó.
Tài liệu của NIST: AES-GCM
Mọi người nên tham khảo ở đây để nắm được đầy đủ cách xây dựng và implement của AES - GCM
Trong bài mình chỉ liệt kê sơ lại các ý chính nên có thể sẽ có nhiều chỗ hơi tắt.

MAC

Một kĩ thuật xác thực dùng khóa bí mật gọi là MAC ( Message Authentication Code). Có thể trình bày ngắn gọn kĩ thuật này như sau:

$A$ và $B$ có chung một khóa bí mật $k$. Khi $A$ muốn gửi thông điệp $P$ cho $B$, $A$ tính toán MAC như sau: $MAC=C_k(P)$. Thông điệp cùng với MAC được gửi cho $B$, sau đó $b$ tiến hành tính toán MAC trên thông điệp nhận được tương tự như $A$ đã tính, sau đó so sánh với MAC nhận được từ $A$.

Nếu như trùng khớp thì:

• $B$ tin chắc rằng thông điệp không bị sửa đổi
• $B$ đảm bảo được rằng thông điệp được gửi một cách hợp pháp từ $A$. Vì chỉ có 2 người sỡ hữu khóa bí mật nên không ai có thể chuẩn bị một thông điệp tương tự

Mã hóa đối xứng như AES cung cấp tính xác thực và được sử dụng rộng rãi nhưng không cung cấp chữ kí số vì cả $A$ và $B$ cùng dùng chung một khóa

Counter Mode

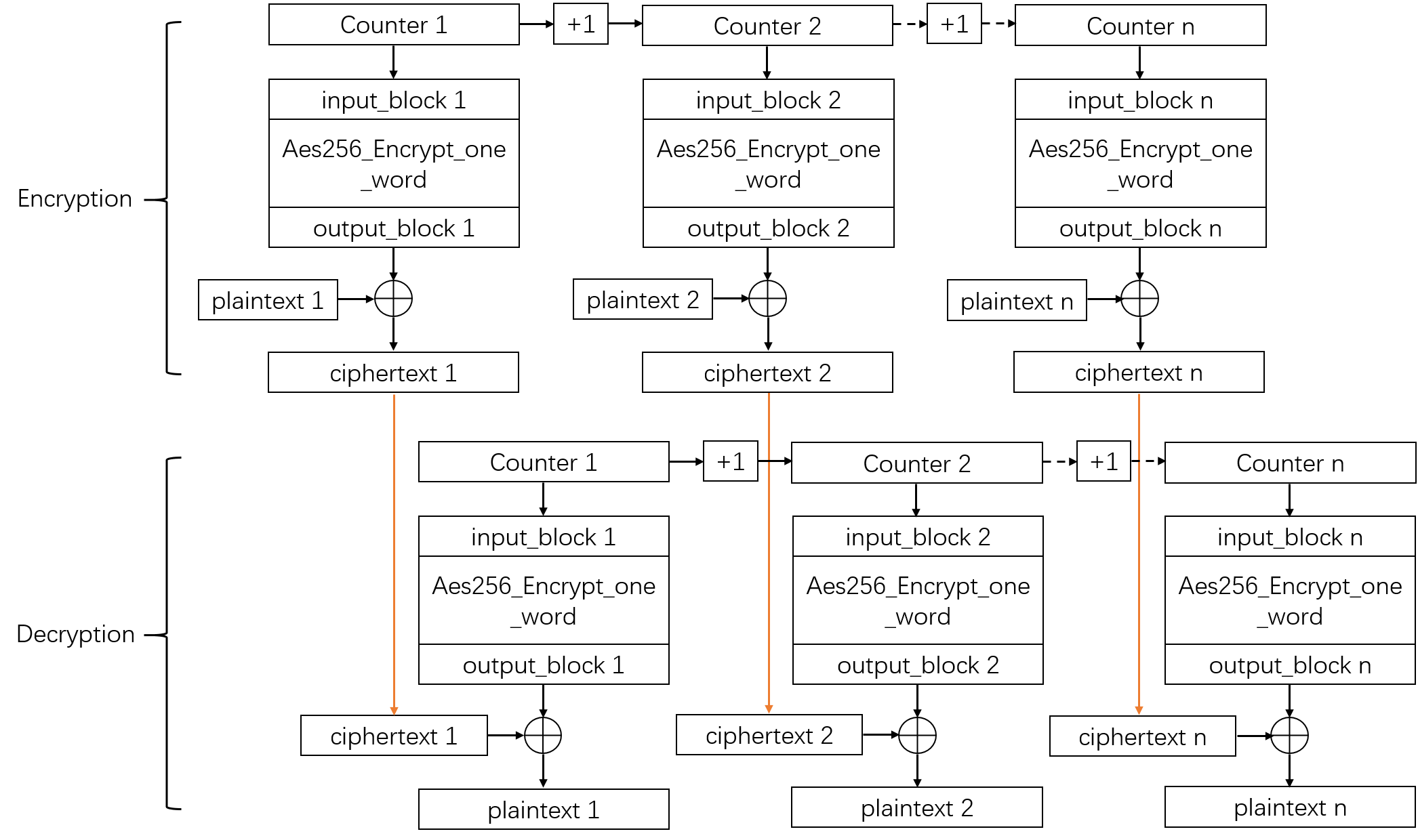
CTR Mode là viết tắt của Counter Mode. CTR là chế độ mã hóa sử dụng một tập các khối ngõ vào, gọi là các counter, để sinh ra một tập các giá trị ngõ ra. Sau đó, giá trị ngõ ra sẽ được XOR với plaintext để tạo ra ciphertext trong quá trình mã hóa, hoặc XOR với ciphertext để tạo ra plaintext trong quá trình giải mã.

Bằng cách này CTR Mode giúp biến AES từ Block Cipher trở thành Stream Cipher. Mọi người có thể xem sơ đồ hoạt động dưới đây của CTR Mode.

Input sẽ bao gồm 2 phần đó là Nonce và một bộ đếm. Nonce là number used once hoặc là IV. Nó sẽ được tạo ra ngẫu nhiên và được sử dụng một lần duy nhất. Ngõ vào của AES Encryption sẽ là Input(i) = Nonce || CTR(i) . Counter sẽ nối vào sau Nonce và Input này sẽ được mã hóa bằng AES với một key $k$. Output sẽ được XOR với Plaintext và tiếp tục như vậy cho các Block khác. CTR(i) sẽ tăng dần khi chuyển sang các Block.

Galois Field

Trước tiên ta cần hiểu trường là gì
Trường. Cho $A$ là một trường nếu như $A$ là một vành giao hoán có đơn vị khác không và mọi phần tử khác không của $A$ đều khả nghịch đối với phép nhân, tức là $A$ là một thể với phép nhân giao hoán.
Vành đa thức hữu hạn biến. Cho $A$ là một vành giao hoán có đơn vị là $1$. Khi đó với một kí hiệu $X$, ta gọi $A[X]$ là tập các biểu thức có dạng

$$f(X)=a_0+a_{1}X+...+a_n{X}^n$$

trong đó $a_i\in A$ với mọi $0⩽i=n,n\in \mathbb{N}$. Giả sử

$$f(X)=a_0+a_{1}X+...+a_n{X}^n,g(X)=b_0+b_{1}X+...+b_n{X}^n\in A[X]$$

Không mất tính tổng quát, ta có thể giả sử $m⩾n$ và $m=n+s$. Khi đó

$$g(X)=b_0+b_{1}X+...+b_n{X}^n+b_{n+1}{X}^{n+1}+...+b_{n+s}{X}^{n+s}$$

Ta định nghĩa phép nhân và phép cộng đơn giản như sau:

Phép cộng:

$$\begin{array}{c}f(X)+g(X)=\sum _{i=0}^n(a_i+b_i)X^i+b_{n+1}{X}^{n+1}+...+b_{n+s}{X}^{n+s}\end{array}$$

Phép nhân:

$$f(X)g(X)=\sum _{i=0}^{m+n}\left(\sum _{j=0}^i{a}_{i-j}{b}_j\right)X^i$$

Vành $A[X]$ được gọi là vành các đa thức của biến $X$ lấy hệ tử trong $A$ (hoặc vành đa thức của biến $X$ trên $A$) còn các phần tử của $A[X]$ được gọi là các đa thức của biến $X$ lấy hệ tử trong $A$. Đa thức

$$f=a_0+a_{1}X+...+a_n{X}^n$$

được gọi là có bậc $n$ và viết là $degf=n$.

Trong AES-GCM các phép tính toán sẽ làm việc trên một trường đặc biệt, kí hiệu là ${\mathbb{F}}_2$. Trường này có đặc số là 2.
Ta cùng đi qua một số ví dụ để hiểu rõ hơn về cách hoạt động của trường này.

Đầu tiên ta có phiên bản đơn giản nhất của nó chính là trường hữu hạn $GF(2)$. Trường này bao gồm 2 phần tử là $0,1$. Phép cộng trên trường này chính là phép XOR logic. Và tương tự phép nhân cũng chính là phép AND logic.

Hiểu đơn giản là ta lấy 2 phần tử trên trường này sau đó thực hiện phép cộng/phép nhân số học như thông thường, sau đó kết quả sẽ được lấy theo modulo 2.

Vì AES-GCM làm việc với các khối có độ lớn là 128 bits cho nên ta cần phải thực hiện tính toán trên trường hữu hạn $GF\left(2^{128}\right)$ gồm có $2^{128}$ phần tử khác nhau.

Để tính toán thì ta cần định nghĩa phép nhân cùng phép cộng trên trường này. Một cách để biểu diễn đó là ta xem các phần tử trong trường $GF\left(2^{128}\right)$ như là một đa thức với các hệ số trong trường ${\mathbb{F}}_2$.

Ví dụ với $1011$ ta sẽ viết lại thành $a(x)=x^3+x+1$.

Như vậy mỗi phần tử trong trường $GF\left(2^{128}\right)$ sẽ được viết dưới dạng nhị phân và mỗi bit sẽ cho ta biết được thông tin là đơn thức $x^i$ có thuộc vào đa thức hay không. Trong GCM thì bit sẽ được viết theo dạng big endian, tức là bit có trọng số cao hơn thì nằm ở trước. Cụ thể, MSB của chuỗi bit sẽ biểu diễn cho $x^0$, bit tiếp theo sẽ là $x^1$ và cứ như vậy cho tới $x^{127}$. Một số ví dụ:

• $1$ sẽ tương đương với $\mathrm{100000....}$

• $x^4+x$ sẽ tương đương với $\mathrm{01001000....}$

Và tương tự.

Tiếp theo ta sẽ định nghĩa phép nhân và cộng trên trường này.

Đối với phép cộng thì ta định nghĩa tương tự như khi làm việc trên trường $GF(2)$ đó là cộng lần lượt từng đơn thức có bậc bằng nhau và sau đó XOR hệ số đứng trước chúng lại. Ví dụ ta có $a(x)=x^2+x\in GF\left(2^{128}\right)$ và $b(x)=x^4+x^2+1\in GF\left(2^{128}\right)$. Ta tính được

$$\begin{array}{c}c(x)=a(x)+b(x)=x^4+\left(x^2+x^2\right)+x+1=x^4+x+1\end{array}$$

Ta chỉ giữ lại những đơn thức nào chỉ xuất hiện tại 1 trong 2 đa thức.

Vì phép cộng được định nghĩa như trên cho nên ta có thể đảm bảo rằng $\mathrm{deg}c⩽127$ và là một đa thức hợp lệ trong trường $GF\left(2^{128}\right)$. Nhưng đối với phép nhân thì phức tạp hơn một chút.

Chẳng hạn ta muốn thực hiện phép nhân giữa $a(x)=x^{126}+x$ và $b(x)=x^3+x^2$. Nếu ta thực hiện phép nhân như thông thường

$$\begin{array}{c}c(x)=a(x)b(x)=x^{129}+x^{128}+x^4+x^3\end{array}$$

Đa thức $c(x)$ thu được có bậc là 129 và rõ ràng không phải là một phần tử hợp lệ trên trường $GF\left(2^{128}\right)$. Để giải quyết vấn đề này thì ta cần sử dụng một đa thức gọi là đa thức bất khả quy để lấy modulo nhằm giảm bậc và đưa $c(x)$ về lại trường $GF\left(2^{128}\right)$. Lý do ta chọn đa thức bất khả quy là để ${\mathbb{F}}_2[X]/q(x)$ tạo thành một trường thương và có một đẳng cấu

$$\begin{array}{c}{\mathbb{F}}_2[X]/q(x)\cong {\mathbb{F}}_{2^{128}}\end{array}$$

Trong GCM thì ta sẽ sử dụng $q(x)=x^{128}+x^7+x^2+x+1$. Hiểu đơn giản thì việc lấy modulo một đa thức bất khả quy tương tự như khi ta lấy modulo một số nguyên tố để tạo ra trường ${\mathbb{F}}_p$ vậy.

Còn thuật toán chia lấy dư thì hơi dài dòng quá nên mình sẽ không đề cập ở đây.

Đầy đủ hơn về phần giải thích này mọi người có thể tham khảo các tài liệu sau:

• https://www.isec.tugraz.at/wp-content/uploads/teaching/mfc/ghash_Kales.pdf
• https://www.lirmm.fr/arith18/papers/kobayashi-AlgorithmInversionUsingPolynomialMultiplyInstruction.pdf

Thuật toán

Sơ đồ thuật toán của GCM như sau:

Toàn bộ quá trình diễn ra như sau: Đối với message có $n$ blocks:

Bước 1. Khởi tạo một $IV$ có độ dài 96 bits
Bước 2. Counter block $J_i$ sau đó sẽ được tạo bằng cách lấy $J_i=IV||cnt$ và $cnt=(i+1)\mathrm{mod}{2}^{32}$ với mỗi $i\in \{1,...,n\}$
Bước 3. Mỗi ciphertext sẽ được tính bởi $C_i=P_i\oplus En{c}_k(J_i)$ trong đó $En{c}_k$ là AES-Encryptor với key là $k$.

Tiếp đến là hàm GHASH. Để tính tag $T$ của AES-GCM thì ta cần sử dụng một hàm gọi là GHASH. Cụ thể cách hoạt động như sau:

Đầu vào của GHASH cần một authenticated key $H$ có độ dài 128 bits. Key $H$ được tạo bằng cách mã hóa 16 NULL bytes bằng AES với key $k$. Sau đó giá trị này sẽ được chuyển thành đa thức và được sử dụng trong suốt quá trình tính toán GHASH.

Để tính, ta cần chuyển dữ liệu cần xác thực thành các khối 128 bits, và sẽ pad thêm các NULL bytes nếu như chưa đạt đủ chiều dài mong muốn. Ta sẽ làm tương tự với additional authenticated data.

Thông tin cuối cùng mà ta cần thêm vào đó là độ lớn của data. Ta sẽ thêm vào một block ở cuối chứa thông tin về độ dài của additional authenticated data và ciphertext.

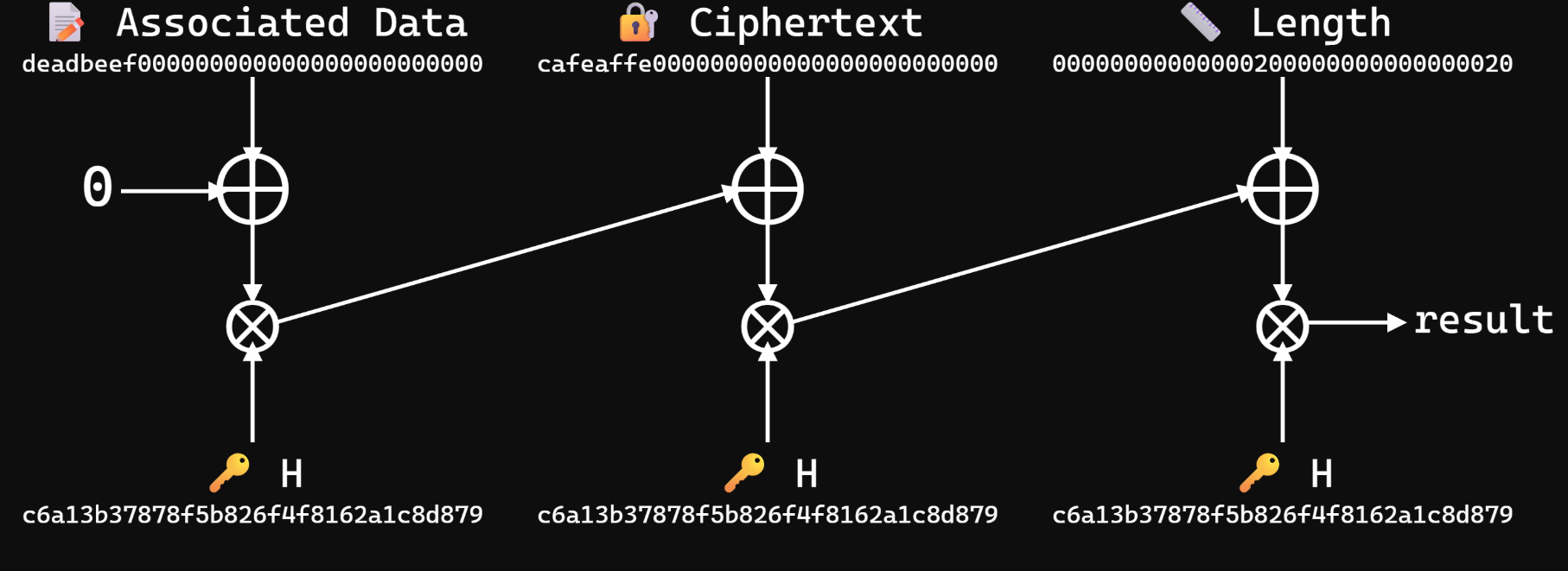
Ở vòng đầu tiên ta sẽ khởi tạo một phần tử $Q\in GF\left(2^{128}\right)$ và $Q=0$. Sau đó ta sẽ lấy giá trị này cộng với AAD. Kết quả sau đó được nhân với key $H$ và trở thành đầu vào cho vòng tiếp theo và cứ thế lặp lại.
Giả sử ta cần tính cho 3 block $U_0,U_1,U_2$.
Ở bước đầu tiên ta sẽ có được $Q\leftarrow U_0\times H$. Sang bước thứ hai ta sẽ có $Q\leftarrow (Q+U_1)\times H$.
Cứ như vậy ta sẽ được

$$\begin{array}{c}Q=((((U_0\times H)+U_1)\times H)+U_2)\times H\\ \to Q=\left(\left(U_0\times H^2+U_1\times H\right)+U_2\right)\times H\\ Q=U_0\times H^3+U_1\times H^2+U_2\times H\end{array}$$

Tag $T$ sau đó sẽ được tính bởi $T=Q+En{c}_k(J_0)$.
Một vài trường hợp có thể sẽ không có AAD ở đầu.
Công thức tổng quát sẽ là như sau:
Với $H=E_K(0^{128}),s=E_K(J_0)$ với $J_0=nonce||0^{31}||1$ . Tiếp theo, tạo các block $A_1,...,A_m$ từ AAD và $C_1,C_2,...,C_n$ từ ciphertext (được nullpad) và block độ dài $L$, thì lúc này ta có

$$tag=S\oplus s$$

với $s$ là keystream cho block này và $S$ được tính bởi:

$$S=\sum _{i=1}^m{A}_i\cdot H^{m+n+1-i}\oplus \sum _{j=1}^n{C}_j\cdot H^{n+1-j}\oplus L\cdot H$$

Implement cho phần trên:

a = GF(2)['a'].gen()
F = GF(2**128, name = 'x' ,modulus = a**128+a**7+a**2+a+1)
def nullpad(msg):
    return bytes(msg) + b'\x00' *(-len(msg) % 16)
def un_nullpad(msg):
    return bytes(msg).strip(b'\x00')
c = b'test'
assert un_nullpad(nullpad(c)) == c 
 
 
def bytes_to_n(b):
    v = int.from_bytes(nullpad(b),'big')
    return int(f"{v:0128b}"[::-1],2)
def bytes_to_poly(b):
    return F.from_integer(bytes_to_n(b))
def poly_to_n(p):
    v = p.to_integer()
    return int(f"{v:0128b}"[::-1],2)
def poly_to_bytes(p):
    return poly_to_n(p).to_bytes(16,'big')
def length_block(lad, lct):
    return int(lad * 8).to_bytes(8, 'big') + int(lct * 8).to_bytes(8, 'big')
def ghash(H, A, C):
    X = F(0)
    for i in range(0, len(A) + (-len(A) % 16), 16):
        B = (A + b'\x00'*16)[i:i+16]
        X = (X + bytes_to_poly(B)) * H
    for i in range(0, len(C) + (-len(C) % 16), 16):
        B = (C + b'\x00'*16)[i:i+16]
        X = (X + bytes_to_poly(B)) * H
    L = bytes_to_poly(length_block(len(A),len(C)))
    X = (X + L) * H
    return X
 
def calculate_tag(key, ct, nonce, ad):
    assert len(nonce) == 12
    E = AES.new(key, AES.MODE_ECB).encrypt
    H = bytes_to_poly(E(b'\x00'*16))
    J0 = nonce + b'\x00\x00\x00\x01'
    S  = ghash(H, ad, ct)
    tag = S + bytes_to_poly(E(J0))
    return poly_to_bytes(tag)
 
def check():
    key = os.urandom(16)
    nonce = os.urandom(12)
 
    ad = os.urandom(os.urandom(1)[0])
    pt = os.urandom(os.urandom(1)[0])
    
    cipher = AES.new(key, AES.MODE_GCM, nonce)
    cipher.update(ad)
    ct, tag = cipher.encrypt_and_digest(pt)
 
    assert tag == calculate_tag(key, ct, nonce, ad)
    print("OK")

Tham khảo thêm tại đây: https://frereit.de/aes_gcm/

Nonce Reuse

Ta đã biết cách AES-GCM tạo tag $T$. Vậy chuyện gì sẽ xảy ra nếu như ta tạo tag cho 2 messages khác nhau mà vẫn giữ nguyên nonce.

Giả sử ta muốn tính $T_1,T_2$ bằng cách sử dụng lại cùng một key và nonce.

Với messages đầu tiên ta sẽ có các block $U{1}_0,U{1}_1,U{1}_2$ và tương tự $U{2}_0,U{2}_1,U{2}_2$.

Ta có

$$\begin{array}{c}T1=U{1}_0\times H^3+U{1}_1\times H^2+U{1}_2\times H+S(S=En{c}_k(J_0))\\ T2=U{2}_0\times H^3+U{2}_1\times H^2+U{2}_2\times H+S\end{array}$$

Vì dùng chung nonce cho nên keystream $S$ đầu tiên là giống nhau. Như vậy ta có thể làm triệt tiêu đi giá trị này bằng cách cộng hai tag lại với nhau

$$\begin{array}{c}T1+T2=(U{1}_0+U{2}_0)\times H^3+(U{1}_0+U{2}_0)\times H^2+(U{1}_0+U{2}_0)\times H\end{array}$$

Ta có thể biết được giá trị của $T1,T2$ cũng như $U1,U2$. Bây giờ nếu ta xem biểu thức trên như một đa thức theo $H$ thì ta có thể giải tìm nghiệm và khôi phục lại được $H$. Việc tìm lại $H$ giúp ta giả mạo được tin nhắn của người gửi bằng cách tính lại GHASH của tin nhắn đó.

Tiếp theo ta sẽ giải quyết một số challenge về AES-GCM

CTF Challenges

CryptoHack Forbidden Fruit

Source code của bài:

from Crypto.Cipher import AES
import os
 
 
IV = ?
KEY = ?
FLAG = ?
 
 
@chal.route('/forbidden_fruit/decrypt/<nonce>/<ciphertext>/<tag>/<associated_data>/')
def decrypt(nonce, ciphertext, tag, associated_data):
    ciphertext = bytes.fromhex(ciphertext)
    tag = bytes.fromhex(tag)
    header = bytes.fromhex(associated_data)
    nonce = bytes.fromhex(nonce)
 
    if header != b'CryptoHack':
        return {"error": "Don't understand this message type"}
 
    cipher = AES.new(KEY, AES.MODE_GCM, nonce=nonce)
    encrypted = cipher.update(header)
    try:
        decrypted = cipher.decrypt_and_verify(ciphertext, tag)
    except ValueError as e:
        return {"error": "Invalid authentication tag"}
 
    if b'give me the flag' in decrypted:
        return {"plaintext": FLAG.encode().hex()}
 
    return {"plaintext": decrypted.hex()}
 
 
@chal.route('/forbidden_fruit/encrypt/<plaintext>/')
def encrypt(plaintext):
    plaintext = bytes.fromhex(plaintext)
    header = b"CryptoHack"
 
    cipher = AES.new(KEY, AES.MODE_GCM, nonce=IV)
    encrypted = cipher.update(header)
    ciphertext, tag = cipher.encrypt_and_digest(plaintext)
 
    if b'flag' in plaintext:
        return {
            "error": "Invalid plaintext, not authenticating",
            "ciphertext": ciphertext.hex(),
        }
 
    return {
        "nonce": IV.hex(),
        "ciphertext": ciphertext.hex(),
        "tag": tag.hex(),
        "associated_data": header.hex(),
    }

Phân tích source code: Bài gồm 2 route là decrypt và encrypt. Hàm encrypt sẽ nhận đầu vào của ta dưới dạng hex sau đó sẽ trả về ciphertext cùng với tag và có thêm một điều kiện là trong plaintext của ta không được chứa b'flag'. Server sẽ trả về lại cho ta nonce, ciphertext, tag và AAD. AAD và nonce trong bài này là cố định và không thay đổi và để lấy được flag thì ta cần forge đoạn tin nhắn chứa b'give me the flag'.

Quá trình tính toán như sau: Đầu tiên ta có

$$\begin{array}{c}T1=A{H}^3+c_1{H}^2+LH+S\\ T2=A{H}^3+c_2{H}^2+LH+S\end{array}$$

trong đó $c_1,c_2$ là hai ciphertext.

Xét

$$\begin{array}{c}{T}_1-c_1{H}^2=T_2-c_2{H}^2\end{array}$$

Ta muốn tính $T_3$ của bản mã $c_3$ thì ta sẽ có được

$$\begin{array}{c}{T}_3-c_3{H}^2=T_1-c_1{H}^2=T_2-c_2{H}^2=X\end{array}$$

Như vậy $T_3=X+c_3{H}^2$. Ta có được $X$ và $H$ như sau:

$$\begin{array}{c}{H}^2=\frac{T_1-T_2}{c_1-c_2}\end{array}$$

Như vậy ta sẽ tính lại được $T_3$. Còn về phần $c_3$ ta có thể gửi lên route encrypt để lấy về. Code giải như sau:

from sage.all import *
from Crypto.Util.number import bytes_to_long, long_to_bytes
from Crypto.Cipher import AES 
from pwn import * 
from tqdm import tqdm 
import requests 
import json 
 
context.log_level = 'debug'
 
# helper functions
 
a = GF(2)['a'].gen()
F = GF(2**128, name = 'x' ,modulus = a**128+a**7+a**2+a+1)
def nullpad(msg):
    return bytes(msg) + b'\x00' *(-len(msg) % 16)
def un_nullpad(msg):
    return bytes(msg).strip(b'\x00')
c = b'test'
assert un_nullpad(nullpad(c)) == c 
 
def bytes_to_n(b):
    v = int.from_bytes(nullpad(b),'big')
    return int(f"{v:0128b}"[::-1],2)
def bytes_to_poly(b):
    return F.from_integer(bytes_to_n(b))
def poly_to_n(p):
    v = p.to_integer()
    return int(f"{v:0128b}"[::-1],2)
def poly_to_bytes(p):
    return poly_to_n(p).to_bytes(16,'big')
def length_block(lad, lct):
    return int(lad * 8).to_bytes(8, 'big') + int(lct * 8).to_bytes(8, 'big')
 
def calculate_tag(key, ct, nonce, ad):
    y = AES.new(key, AES.MODE_ECB).encrypt(bytes(16))
    s = AES.new(key, AES.MODE_ECB).encrypt(nonce + b"\x00\x00\x00\x01")
    assert len(nonce) == 12
    y = bytes_to_poly(y)
 
    l = length_block(len(ad), len(ct))
 
    blocks = nullpad(ad) + nullpad(ct)
    bl = len(blocks) // 16
 
    blocks = [blocks[16 * i:16 * (i + 1)] for i in range(bl)]
    blocks.append(l)
    blocks.append(s)
 
    tag = F(0)
    
    for exp, block in enumerate(blocks[::-1]):
        tag += y**exp * bytes_to_poly(block)
 
    tag = poly_to_bytes(tag)
 
    return tag
 
# def check():
#     key = os.urandom(16)
#     nonce = os.urandom(12)
 
#     ad = os.urandom(os.urandom(1)[0])
#     pt = os.urandom(os.urandom(1)[0])
    
#     cipher = AES.new(key, AES.MODE_GCM, nonce)
#     cipher.update(ad)
#     ct, tag = cipher.encrypt_and_digest(pt)
 
#     assert tag == calculate_tag(key, ct, nonce, ad)
 
# if __name__ == "__main__":
#     check()
 
def solve():
    def encrypt(plaintext):
        url = 'http://aes.cryptohack.org/forbidden_fruit/encrypt/'
        url += plaintext.hex()
        r = requests.get(url).json()
        if "error" in r:
            return None, bytes.fromhex(r["ciphertext"])
        return bytes.fromhex(r["nonce"]), bytes.fromhex(r["ciphertext"]), bytes.fromhex(r["tag"]), bytes.fromhex(r["associated_data"])
    def decrypt(nonce,ciphertext,tag,associated_data):
        url = 'http://aes.cryptohack.org/forbidden_fruit/decrypt/'
        url += nonce.hex() + '/' + ciphertext.hex() + '/' + tag + '/' + associated_data.hex()
        r = requests.get(url).json()
        return bytes.fromhex(r["plaintext"])
    msg1 = b'\x00' * 16
    msg2 = b'\x01' * 16
    r1 = encrypt(msg1)
    r2 = encrypt(msg2)
    A = r1[3]
    print(A)
    nonce = r1[0]
    c1, T1 = r1[1], r1[2]
    c2, T2 = r2[1], r2[2]
    c1 = bytes_to_poly(c1)
    c2 = bytes_to_poly(c2)
    T1 = bytes_to_poly(T1)
    T2 = bytes_to_poly(T2)
    H_2 = (T1-T2)/(c1-c2)
    assert T1 - c1*H_2 == T2 - c2*H_2
    X = T1 - c1*H_2
    msg3 = b'give me the flag'
    c3 = encrypt(msg3)[1]
    T3 = X + bytes_to_poly(c3)*H_2 
    print(T3)
    tag3 = poly_to_n(T3)
    print(decrypt(nonce, c3, hex(tag3)[2:],A).decode())
if __name__ == "__main__":
    solve()

Securinets CTF 2025 - Fl1pper Zer0

Source code của bài:

from Crypto.Util.number import long_to_bytes, bytes_to_long, inverse
from Crypto.Cipher import AES
from Crypto.Util.Padding import pad
from fastecdsa.curve import P256 as EC
from fastecdsa.point import Point
import os, random, hashlib, json
from secret import FLAG
 
class SignService:
    def __init__(self):
        self.G = Point(EC.gx, EC.gy, curve=EC)
        self.order = EC.q
        self.p = EC.p
        self.a = EC.a
        self.b = EC.b
        self.privkey = random.randrange(1, self.order - 1)
        self.pubkey = (self.privkey * self.G)
        self.key = os.urandom(16)
        self.iv = os.urandom(16)
 
    def generate_key(self):
        self.privkey = random.randrange(1, self.order - 1)
        self.pubkey = (self.privkey * self.G)
 
    def ecdsa_sign(self, message, privkey):
        z = int(hashlib.sha256(message).hexdigest(), 16)
        k = random.randrange(1, self.order - 1)
        r = (k*self.G).x % self.order
        s = (inverse(k, self.order) * (z + r*privkey)) % self.order
        return (r, s)
 
    def ecdsa_verify(self, message, r, s, pubkey):
        r %= self.order
        s %= self.order
        if s == 0 or r == 0:
            return False
        z = int(hashlib.sha256(message).hexdigest(), 16)
        s_inv = inverse(s, self.order)
        u1 = (z*s_inv) % self.order
        u2 = (r*s_inv) % self.order
        W = u1*self.G + u2*pubkey
        return W.x == r
 
    def aes_encrypt(self, plaintext):
        cipher = AES.new(self.key, AES.MODE_GCM, nonce=self.iv)
        ct, tag = cipher.encrypt_and_digest(plaintext)
        return tag + ct
 
    def aes_decrypt(self, ciphertext):
        tag, ct = ciphertext[:16], ciphertext[16:]
        cipher = AES.new(self.key, AES.MODE_GCM, nonce=self.iv)
        plaintext = cipher.decrypt_and_verify(ct, tag)
        return plaintext
 
    def get_flag(self):
        key = hashlib.sha256(long_to_bytes(self.privkey)).digest()[:16]
        cipher = AES.new(key, AES.MODE_ECB)
        encrypted_flag = cipher.encrypt(pad(FLAG.encode(), 16))
        return encrypted_flag
 
 
if __name__ == '__main__':
    print("Welcome to Fl1pper Zer0 – Signing Service!\n")
 
    S = SignService()
 
    signkey = S.aes_encrypt(long_to_bytes(S.privkey))
 
    print(f"Here is your encrypted signing key, use it to sign a message : {json.dumps({'pubkey': {'x': hex(S.pubkey.x), 'y': hex(S.pubkey.y)}, 'signkey': signkey.hex()})}")
 
    while True:
        print("\nOptions:\n \
    1) sign <message> <signkey> : Sign a message\n \
    2) verify <message> <signature> <pubkey> : Verify the signed message\n \
    3) generate_key : Generate a new signing key\n \
    4) get_flag : Get the flag\n \
    5) quit : Quit\n")
 
        try:
            inp = json.loads(input('> '))
 
            if 'option' not in inp:
                print(json.dumps({'error': 'You must send an option'}))
 
            elif inp['option'] == 'sign':
                msg = bytes.fromhex(inp['msg'])
                signkey = bytes.fromhex(inp['signkey'])
                sk = bytes_to_long(S.aes_decrypt(signkey))
 
                r, s = S.ecdsa_sign(msg, sk)
                print(json.dumps({'r': hex(r), 's': hex(s)}))
 
            elif inp['option'] == 'verify':
                msg = bytes.fromhex(inp['msg'])
                r = int(inp['r'], 16)
                s = int(inp['s'], 16)
                px = int(inp['px'], 16)
                py = int(inp['py'], 16)
                pub = Point(px, py, curve=EC)
 
                verified = S.ecdsa_verify(msg, r, s, pub)
 
                if verified:
                    print(json.dumps({'result': 'Success'}))
                else:
                    print(json.dumps({'result': 'Invalid signature'}))
 
            elif inp['option'] == 'generate_key':
                S.generate_key()
                signkey = S.aes_encrypt(long_to_bytes(S.privkey))
                print("Here is your *NEW* encrypted signing key :")
                print(json.dumps({'pubkey': {'x': hex(S.pubkey.x), 'y': hex(S.pubkey.y)}, 'signkey': signkey.hex()}))
 
            elif inp['option'] == 'get_flag':
                encrypted_flag = S.get_flag()
                print(json.dumps({'flag': encrypted_flag.hex()}))
 
            elif inp['option'] == 'quit':
                print("Adios :)")
                break
 
            else:
                print(json.dumps({'error': 'Invalid option'}))
 
        except Exception:
            print(json.dumps({'error': 'Oops! Something went wrong'}))
            break

Phân tích source code:

Padding Oracle Attack

Pad Thai

Source code của bài:

#!/usr/bin/env python3
 
from Crypto.Util.Padding import unpad
from Crypto.Cipher import AES
from os import urandom
 
from utils import listener
 
FLAG = 'crypto{?????????????????????????????????????????????????????}'
 
class Challenge:
    def __init__(self):
        self.before_input = "Let's practice padding oracle attacks! Recover my message and I'll send you a flag.\n"
        self.message = urandom(16).hex()
        self.key = urandom(16)
 
    def get_ct(self):
        iv = urandom(16)
        cipher = AES.new(self.key, AES.MODE_CBC, iv=iv)
        ct = cipher.encrypt(self.message.encode("ascii"))
        return {"ct": (iv+ct).hex()}
 
    def check_padding(self, ct):
        ct = bytes.fromhex(ct)
        iv, ct = ct[:16], ct[16:]
        cipher = AES.new(self.key, AES.MODE_CBC, iv=iv)
        pt = cipher.decrypt(ct)  # does not remove padding
        try:
            unpad(pt, 16)
        except ValueError:
            good = False
        else:
            good = True
        return {"result": good}
 
    def check_message(self, message):
        if message != self.message:
            self.exit = True
            return {"error": "incorrect message"}
        return {"flag": FLAG}
 
    #
    # This challenge function is called on your input, which must be JSON
    # encoded
    #
    def challenge(self, msg):
        if "option" not in msg or msg["option"] not in ("encrypt", "unpad", "check"):
            return {"error": "Option must be one of: encrypt, unpad, check"}
 
        if msg["option"] == "encrypt": return self.get_ct()
        elif msg["option"] == "unpad": return self.check_padding(msg["ct"])
        elif msg["option"] == "check": return self.check_message(msg["message"])
 
import builtins; builtins.Challenge = Challenge # hack to enable challenge to be run locally, see https://cryptohack.org/faq/#listener
listener.start_server(port=13421)

Phân tích:

Ta sẽ xem xét các hàm trong class Challenge.
Đầu tiên là hàm get_ct . Một initial vector được tạo ra bởi urandom(16). Cipher AES được khởi tạo cùng với iv này và key có từ trước. Sau đó nó sẽ encrypt msg bằng cipher mới này và trả về kết quả là (iv+ct).hex().

Hàm tiếp theo là hàm check_padding .

Đầu vào là ct và sau đó gọi hàm unpad để kiểm tra xem padding có hợp lệ hay chưa. Đây có thể xem như là oracle để thực hiện padding oracle attacks.

Hàm cuối cùng là check_message. Nếu như msg ta nhập vào bằng đúng với self.message của bài thì server sẽ trả về flag.

Như vậy, server cho ta 3 option. Một là gọi encrypt để lấy lại ct. Hai là unpad để check padding và cuối cùng là check sau khi ta khôi phục lại được msg.

Nhắc lại và giải thích Padding Oracle Attacks:

Ở bài này server sử dụng CBC Mode:

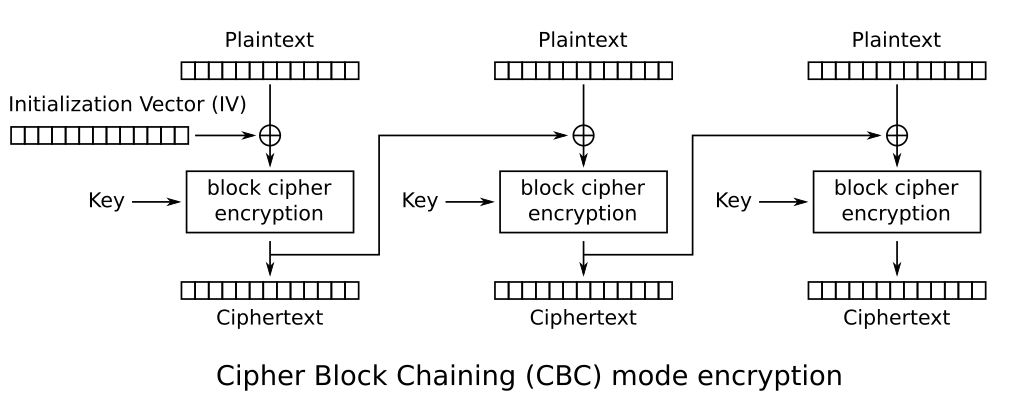
CBC mã hóa msg bằng cách chia nó thành các block có độ dài 16 bytes. Khối đầu tiên được XOR với IV và đưa vào hàm mã hóa ${\text{Enc}}_{AES}(key,p{t}_1\oplus iv)$. Kết quả của block đầu tiên này được sử dụng để XOR với block plaintext tiếp theo và cứ thế lặp lại. Để giải mã thì ta làm ngược lại quá trình trên.

Thuật toán padding được sử dụng trong CBC đó là PKCS#7. Nó hoạt động khá đơn giản bằng cách pad thêm vào sau plaintext các bytes bằng chính số bytes còn thiếu.

Chẳng hạn nếu block của ta chỉ có 15 bytes thì nó sẽ pad thêm ở cuối giá trị \\x01 .

PKCS7

Bây giờ để decrypt lại plaintext thì ta làm như sơ đồ dưới đây:

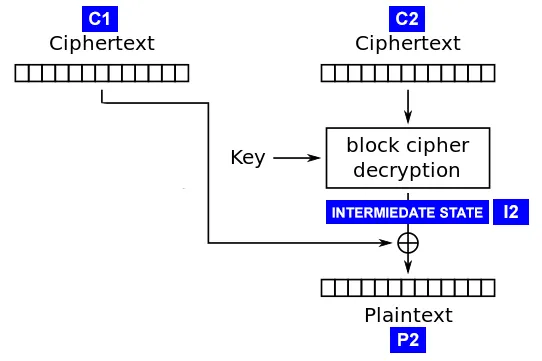
Ý tưởng của Attack như sau:

Ta biết được giá trị của C1 và C2. Nếu như bây giờ ta biết được giá trị của I2 thì ta có thể giải mã và tìm lại được P2.

Oracle của ta sẽ nhận vào ciphertext bất kì, và thông báo cho ta biết liệu padding đã hợp lệ hay chưa.

Như vậy ta có thể tùy ý điều chỉnh giá trị của C1'+C2 và gửi đến server.

Bây giờ ta gọi P2' là plaintext giả được giải mã từ ciphertext giả mạo ở trên.

• Đầu tiên ta tạo ciphertext giả mạo là C1' gồm có C1'[1:15] là các random bytes và C1'[16] sẽ là 00. Nếu như kết quả giải mã C1'+C2 trả về valid padding thì ta có thể biết được rằng P2'[16]=01. Nếu như không là valid padding thì ta sẽ tiếp tục lặp C1'[16] cho tới khi kết quả trả về là valid padding.

Lí do tại sao lại như vậy? Trước hết nếu như ta làm như vậy thì ta sẽ tính lại được I2[16] bằng cách lấy XOR giữa C1'[16] và P2'[16] vì ta đã biết hai giá trị này.

Bây giờ ta sẽ tìm hiểu tại sao lại như vậy. Giả sử plaintext ban đầu được pad có dạng b'msg\\x02\\x02`` gồm 2 bytes ở cuối. Nhưng khi ta thay đổi bytes cuối của C1’[16]thì sao? Kết quả giải mãC2` bằng AES vẫn như cũ nhưng khi XOR với một giá trị không hợp lệ khác thì msg được trả về sẽ không còn theo đúng định dạng PKCS#7 Padding.

PKCS#7 có một điểm đặc biệt đó là kể cả khi msg đủ 16 bytes thì nó vẫn thực hiện pad thêm 16 bytes ở sau. Ví dụ như

from Crypto.Util.Padding import pad, unpad
from os import urandom
msg = b'11'*16
new_msg = pad(msg,16)
print(new_msg)
# b'11111111111111111111111111111111\\x10\\x10\\x10\\x10\\x10\\x10\\x10\\x10\\x10\\x10\\x10\\x10\\x10\\x10\\x10\\x10'

Như vậy, nếu như plaintext thu được khi sử dụng một block giả mạo như C1' được đưa vào hàm unpad thì trừ khi bytes cuối là 01 nếu không thì nó sẽ không unpad được và sẽ báo không hợp lệ. Tương tự, nếu muốn khôi phục lại bytes tiếp theo sau đó thì ta sẽ chọn C1'[16] sao cho khi nó XOR với I2[16] đã biết ra kết quả là 02 và brute bytes còn lại của IV là C1'[15] cho tới khi valid padding là được. Đó là ý tưởng chính.

from pwn import *
import json 
r = remote("socket.cryptohack.org", 13421)
r.recvline()
def oracle(ct_hex):
    payload = json.dumps({"option":"unpad", "ct":ct_hex}).encode()
    r.sendline(payload)
    response = r.recvline()
    result = json.loads(response.decode())
    return result["result"]
def get_ct():
    payload = json.dumps({"option":"encrypt"}).encode()
    r.sendline(payload)
    response = r.recvline()
    result = json.loads(response.decode()) 
    return result["ct"] 
def get_flag(msg):
    payload = json.dumps({"option":"check", "message":msg}).encode()
    r.sendline(payload)
    response = r.recvline()
    result = json.loads(response.decode())
    return result
 
from Crypto.Util.strxor import strxor
def attack(iv,ciphertext):
    dec = bytearray(16)
    for i in range(15,-1,-1):
        padding = 16 - i 
        suffix = bytes([b^padding for b in dec[i+1:]])
        for b in range(256):
            guess = b.to_bytes(1,'big')
            fake_iv = b'\x00' * i + guess + suffix
            ct = (fake_iv + ciphertext).hex()
            if oracle(ct): 
                dec[i] = b^padding
                print(dec)
                break
        else:
            raise ValueError
    return strxor(iv,bytes(dec))
data = get_ct()
ct_bytes = bytes.fromhex(data)
iv = ct_bytes[:16]
ct = ct_bytes[16:]
ct1 = ct[:16]
ct2 = ct[16:]
p1 = attack(iv,ct1)
p2 = attack(ct1,ct2)
print(p1+p2)
print(get_flag((p1 + p2).hex()))
# {'flag': 'crypto{if_you_ask_enough_times_you_usually_get_what_you_want}'}        

The Good, The Pad, The Ugly

Source code của bài:

from Crypto.Util.Padding import unpad
from Crypto.Cipher import AES
from os import urandom
from random import SystemRandom
 
from utils import listener
 
FLAG = 'crypto{??????????????????????????????????????????}'
rng = SystemRandom()
 
 
class Challenge:
    def __init__(self):
        self.before_input = "That last challenge was pretty easy, but I'm positive that this one will be harder!\n"
        self.message = urandom(16).hex()
        self.key = urandom(16)
        self.query_count = 0
        self.max_queries = 12_000
 
    def update_query_count(self):
        self.query_count += 1
        if self.query_count >= self.max_queries:
            self.exit = True
 
    def get_ct(self):
        iv = urandom(16)
        cipher = AES.new(self.key, AES.MODE_CBC, iv=iv)
        ct = cipher.encrypt(self.message.encode("ascii"))
        return {"ct": (iv+ct).hex()}
 
    def check_padding(self, ct):
        ct = bytes.fromhex(ct)
        iv, ct = ct[:16], ct[16:]
        cipher = AES.new(self.key, AES.MODE_CBC, iv=iv)
        pt = cipher.decrypt(ct)  # does not remove padding
        try:
            unpad(pt, 16)
        except ValueError:
            good = False
        else:
            good = True
        self.update_query_count()
        return {"result": good | (rng.random() > 0.4)}
 
    def check_message(self, message):
        if message != self.message:
            self.exit = True
            return {"error": "incorrect message"}
        return {"flag": FLAG}
 
    #
    # This challenge function is called on your input, which must be JSON
    # encoded
    #
    def challenge(self, msg):
        if "option" not in msg or msg["option"] not in ("encrypt", "unpad", "check"):
            return {"error": "Option must be one of: encrypt, unpad, check"}
 
        if msg["option"] == "encrypt": return self.get_ct()
        elif msg["option"] == "unpad": return self.check_padding(msg["ct"])
        elif msg["option"] == "check": return self.check_message(msg["message"])
 
 
import builtins; builtins.Challenge = Challenge # hack to enable challenge to be run locally, see https://cryptohack.org/faq/#listener
listener.start_server(port=13422)

Bài này giống hệt bài trên kia, cũng là padding oracle attacks nhưng có một vấn đề đó là nó thêm vào 2 điều kiện. Điều kiện đầu tiên là không được truy vấn quá 12000 lần. Điều kiện thứ hai là ở hàm (rng.random() > 0.4), hàm này sẽ trả về True với xác suất là 60% còn False với xác suất là 40%.

Toán tử | là toán tử OR tức là chỉ cần 1 trong 2 True thì kết quả sẽ trả về là True. Nếu padding hợp lệ thì nó trả về True, ngược lại nếu padding không hợp lệ thì vẫn có xác suất nó trả về True.

Vậy thì ta nên xử lí như thế nào? Xác suất để padding không hợp lệ nhưng vẫn trả về True là 60%

Ý tưởng.

Oracle	RNG	Output	Prob
1	0 (<0.4)	1	40
1	1 (>0.4)	1	60
0	1	1	60
0	0	0	40

Như đã thấy ở trên thì nếu padding là đúng thì mặc cho kết quả là gì Oracle vẫn sẽ trả về kết quả là đúng. Trong khi đó, nếu như padding sai thì server sẽ trả về kết quả sai với xác suất là $0.6$.

Vậy ta sẽ thử nhiều lần. Giả sử ở lần thử đầu tiên ta được kết quả sai với xác suất là $0.6$. Do các phép thử là độc lập cho nên xác suất để oracle trả về kết quả sai ở lần thử tiếp theo sẽ là $(0.6{)}^2$. Và khi thử $n$ lần thì xác suất sai sẽ là $(0.6{)}^n$.

Khi $n$ càng lớn thì xác suất xảy ra sai sót sẽ càng giảm và trở nên không đáng kể. Như vậy để giải bài này, với mỗi fake IV mà ta tạo ra, ta sẽ gửi tới server để kiểm tra tổng cộng $n$ lần. Nếu như tổng cộng $n$ lần liên tiếp đều True thì ta có thể kết luận với xác suất đáng kể rằng padding là hợp lệ. Ngược lại nếu như trong số $n$ lần có ít nhất một lần server phản hồi sai thì padding là sai và ta loại trường hợp này. Ta được truy vấn tối đa 12000 lần, có 256 bytes cần brute và ta cần làm 2 lần với 2 block khác nhau cho nên có kiểm tra với số phép thử là $12000:(256\ast 2)\approx 23$ lần.

Với mỗi ciphertext, ta gọi lên oracle 23 lần, nếu cả 23 lần đều True thì khả năng cao là đúng còn ngược lại là sai (tức là cả 23 lần trên thực tế đều là invalid padding nhưng oracle trả về là True, xác suất để điều này xảy ra là rất thấp)

Solve script:

from pwn import *
import json 
r = remote("socket.cryptohack.org", 13422)
r.recvline()
def check23(ct_hex, tries=23):
    for _ in range(tries):
        if not oracle(ct_hex):
            return False
    return True
def oracle(ct_hex):
    global queries
    queries += 1
    payload = json.dumps({"option":"unpad", "ct":ct_hex}).encode()
    r.sendline(payload)
    response = r.recvline()
    result = json.loads(response.decode())
    return result["result"]
def get_ct():
    payload = json.dumps({"option":"encrypt"}).encode()
    r.sendline(payload)
    response = r.recvline()
    result = json.loads(response.decode()) 
    return result["ct"] 
def get_flag(msg):
    payload = json.dumps({"option":"check", "message":msg}).encode()
    r.sendline(payload)
    response = r.recvline()
    result = json.loads(response.decode())
    return result
 
from Crypto.Util.strxor import strxor
queries = 0
def attack(iv,ciphertext):
    dec = bytearray(16)
    for i in range(15,-1,-1):
        padding = 16 - i 
        suffix = bytes([b^padding for b in dec[i+1:]])
        for b in range(256):
            guess = b.to_bytes(1,'big')
            fake_iv = b'\x00' * i + guess + suffix
            ct = (fake_iv + ciphertext).hex()
            if check23(ct):
                dec[i] = b ^ padding
                print(f"lần thử thứ {queries} , {dec}")
                break
        else:
            raise ValueError
    return strxor(iv,bytes(dec))
data = get_ct()
ct_bytes = bytes.fromhex(data)
iv = ct_bytes[:16]
ct = ct_bytes[16:]
ct1 = ct[:16]
ct2 = ct[16:]
p1 = attack(iv,ct1)
p2 = attack(ct1,ct2)
print(p1+p2)
flag = get_flag((p1 + p2).decode('ascii'))
print(flag)
# {'flag': 'crypto{even_a_faulty_oracle_leaks_all_information}'}

Oracular Spectacular

Source code của bài:

#!/usr/bin/env python3
 
from Crypto.Util.Padding import unpad
from Crypto.Cipher import AES
from os import urandom
from random import SystemRandom
 
from utils import listener
 
FLAG = 'crypto{????????????????????????????????????????????????????}'
rng = SystemRandom()
 
 
class Challenge:
    def __init__(self):
        self.before_input = "That last challenge was pretty easy, but I'm positive that this one will be harder!\n"
        self.message = urandom(16).hex()
        self.key = urandom(16)
        self.query_count = 0
        self.max_queries = 12_000
 
    def update_query_count(self):
        self.query_count += 1
        if self.query_count >= self.max_queries:
            self.exit = True
 
    def get_ct(self):
        iv = urandom(16)
        cipher = AES.new(self.key, AES.MODE_CBC, iv=iv)
        ct = cipher.encrypt(self.message.encode("ascii"))
        return {"ct": (iv+ct).hex()}
 
    def check_padding(self, ct):
        ct = bytes.fromhex(ct)
        iv, ct = ct[:16], ct[16:]
        cipher = AES.new(self.key, AES.MODE_CBC, iv=iv)
        pt = cipher.decrypt(ct)  # does not remove padding
        try:
            unpad(pt, 16)
        except ValueError:
            good = False
        else:
            good = True
        self.update_query_count()
        return {"result": good ^ (rng.random() > 0.4)}
 
    def check_message(self, message):
        if message != self.message:
            self.exit = True
            return {"error": "incorrect message"}
        return {"flag": FLAG}
 
    #
    # This challenge function is called on your input, which must be JSON
    # encoded
    #
    def challenge(self, msg):
        if "option" not in msg or msg["option"] not in ("encrypt", "unpad", "check"):
            return {"error": "Option must be one of: encrypt, unpad, check"}
 
        if msg["option"] == "encrypt": return self.get_ct()
        elif msg["option"] == "unpad": return self.check_padding(msg["ct"])
        elif msg["option"] == "check": return self.check_message(msg["message"])
 
 
import builtins; builtins.Challenge = Challenge # hack to enable challenge to be run locally, see https://cryptohack.org/faq/#listener
listener.start_server(port=13423)

Tương tự bài kia nhưng có một thay đổi nhỏ. Thay vì dùng phép OR thì giờ đây nó sẽ sử dụng phép XOR good ^ (rng.random() > 0.4).

Bảng chân trị của phép XOR:

A	B	A ^ B
1	0	1
1	1	0
0	0	0
0	1	1

Bây giờ ta xét với giá trị của good và rng.random()>0.4

Oracle	RNG	Output	Prob
1	0	1	0.4
1	1	0	0.6
0	0	0	0.4
0	1	1	0.6

Nhận xét: khi padding là hợp lệ thì vẫn có xác suất để server trả về lỗi thay vì chắc chắn 100% là đúng như ở trên. Do đó ta không thể sử dụng chiến thuật chỉ xét 1 trong hai trường hợp là valid hoặc invalid như bài trên nữa. Tương tự, khi padding là không hợp lệ thì vẫn có xác suất để server trả về đáp án chính xác hoặc không.