Crack Random

Trong mật mã học hiện đại , PRNGS - bộ sinh số giả ngẫu nhiên đóng vai trò quan trọng trong việc tạo ra những dữ liệu trông có vẻ “ngẫu nhiên” như nonce hoặc key. Đối với PRNGS ta có ba khái niệm chung như sau:

Seed: giá trị khởi tạo của PRNG
Internal state: trạng thái của PRNG, lưu trữ các biến số để có thể dự đoán được giá trị và trạng thái tiếp theo của PRNG.
Period: Chu kì của random, random sẽ lặp lại mỗi khi chu kì kết thúc.
Trên thực tế, không phải tất cả các PRNG đều được thiết kế an toàn và với một lượng thông tin nhất định ta có thể crack được bộ sinh và khôi phục lại seed cũng như dự đoán được giá trị tiếp theo của nó.

Link github: https://github.com/ken3k06/crack-random

Python

Source của hàm: https://github.com/python/cpython/blob/23362f8c301f72bbf261b56e1af93e8c52f5b6cf/Modules/_randommodule.c

Mersenne Twister MT19937

Thuật toán cho hàm random của Python được mặc định là Mersenne Twister MT19937

/* Period parameters -- These are all magic.  Don't change. */
#define N 624
#define M 397
#define MATRIX_A 0x9908b0dfU    /* constant vector a */
#define UPPER_MASK 0x80000000U  /* most significant w-r bits */
#define LOWER_MASK 0x7fffffffU  /* least significant r bits */
 
typedef struct {
    PyObject *Random_Type;
    PyObject *Long___abs__;
} _randomstate;
 
static inline _randomstate*
get_random_state(PyObject *module)
{
    void *state = _PyModule_GetState(module);
    assert(state != NULL);
    return (_randomstate *)state;
}
 
static struct PyModuleDef _randommodule;
 
#define _randomstate_type(type) \\
    (get_random_state(_PyType_GetModuleByDef(type, &_randommodule)))
 
typedef struct {
    PyObject_HEAD
    int index;
    uint32_t state[N];
} RandomObject;
 
#include "clinic/_randommodule.c.h"
 
/*[clinic input]
module _random
class _random.Random "RandomObject *" "_randomstate_type(type)->Random_Type"
[clinic start generated code]*/
/*[clinic end generated code: output=da39a3ee5e6b4b0d input=70a2c99619474983]*/
 
/* Random methods */
 
/* generates a random number on [0,0xffffffff]-interval */
static uint32_t
genrand_uint32(RandomObject *self)
{
    uint32_t y;
    static const uint32_t mag01[2] = {0x0U, MATRIX_A};
    /* mag01[x] = x * MATRIX_A  for x=0,1 */
    uint32_t *mt;
 
    mt = self->state;
    if (self->index >= N) { /* generate N words at one time */
        int kk;
 
        for (kk=0;kk<N-M;kk++) {
            y = (mt[kk]&UPPER_MASK)|(mt[kk+1]&LOWER_MASK);
            mt[kk] = mt[kk+M] ^ (y >> 1) ^ mag01[y & 0x1U];
        }
        for (;kk<N-1;kk++) {
            y = (mt[kk]&UPPER_MASK)|(mt[kk+1]&LOWER_MASK);
            mt[kk] = mt[kk+(M-N)] ^ (y >> 1) ^ mag01[y & 0x1U];
        }
        y = (mt[N-1]&UPPER_MASK)|(mt[0]&LOWER_MASK);
        mt[N-1] = mt[M-1] ^ (y >> 1) ^ mag01[y & 0x1U];
 
        self->index = 0;
    }
 
    y = mt[self->index++];
    y ^= (y >> 11);
    y ^= (y << 7) & 0x9d2c5680U;
    y ^= (y << 15) & 0xefc60000U;
    y ^= (y >> 18);
    return y;
}

Một cách tổng quát, thuật toán Mersenne Twister được triển khai bằng đệ quy, bởi biểu thức được gọi là Twist như sau

x_{k + n} := x_{k + m} \oplus ((x_{k}^{w - r} ∣ x_{k + 1}^{r}) A)

Trong đó

$w$ là word length, là độ dài của vector đầu ra $x$
$x$ là một vector $w - bi t s$ , là đầu ra của MT
$n$ là độ dài của dãy $x_{i}$ .
$r$ : điểm chia vector thành 2 phần, phần trái tương ứng với $w - r$ bits và phần bên phải tương đương với $r$ bits.
$A$ là một ma trận vuông kích thước $w \times w$ .
$x_{k}^{w - r}$ gồm $w - r$ bits bên trái của $x_{k}$
$x_{k + 1}^{r}$ gồm $r$ bits bên phải của $x_{k + 1}$ .
$∣$ là phép nối chuỗi bits, nối 2 phần trên lại để tạo thành một vector $w$ bits.

Điều kiện ràng buộc là $2^{n w - r} - 1$ là một số nguyên tố.

Ma trận $A$ được biểu diễn dưới dạng:

A = 00 a_{w - 1} 10 a_{w - 2} 01 ... ... ... ⋱ ... 001 a_{0}

Lí do chọn $A$ như vậy là để phép nhân ma trận trở nên đơn giản và nhanh chóng. Với $x = [x_{w - 1}, ..., x_{0}]$ thì ta có thể tính đơn giản như sau:

xA = {x ≫ 1 (x ≫ 1) \oplus a x_{0} = 0 x_{0} = 1

$a$ là vector ở hàng cuối cùng của $A$ .

Sau khi xây dựng xong dãy các vector $x_{0}, x_{1}, ..., x_{n - 1}$ , để điều chỉnh phân phối của kết quả đầu ra, người ta chọn một ma trận $T$ kích thước $w \times w$ và nhân tiếp vào $x$ để tạo ra một vector $z$ .

z = xT

Quá trình này được gọi là tampering.

Tức là ta thực hiện một biến đổi tuyến tính trên $F_{2}^{w}$ thông qua toán tử tuyến tính là ma trận $T$ . Để đơn giản hóa quá trình người ta sẽ chọn ma trận $T$ sao cho kết quả có thể nhận được chỉ bằng các phép XOR, AND và bit-shift.

y := x \oplus ((x ≫ u) & d) y := y \oplus ((y ≪ s) & b) y := y \oplus (y ≪ t) & c) z := y \oplus (y ≫ l)

Cuối cùng ta nói qua về bước khởi tạo.

Ta cần tạo các giá trị $x$ ban đầu trước khi thuật toán bắt đầu. Với đầu vào là seed, ta sẽ gán cho $x_{0}$ và các giá trị $x_{i}$ sau đó được tính bởi

x_{i} = f \times (x_{i - 1} \oplus (x_{i - 1} ≫ (w - 2))) + i

Trong source code thì các tham số được mặc định như dưới đây:

/* Period parameters -- These are all magic.  Don't change. */
#define N 624
#define M 397
#define MATRIX_A 0x9908b0dfU    /* constant vector a */
#define UPPER_MASK 0x80000000U  /* most significant w-r bits */
#define LOWER_MASK 0x7fffffffU  /* least significant r bits */

Tóm lại các bước của thuật toán sẽ như sau:

Đầu tiên ta cần khởi tạo một mảng rỗng gồm 624 phần tử, phần tử đầu tiên là seed và các phần tử sau đó được sinh ra theo công thức đệ quy ở trên tạo thành state ban đầu.
Mỗi bước sinh số, ta sẽ sinh ra các số theo công thức tampering và sau khi sinh đủ 624 số thì sẽ đưa vào hàm Twist để tính toán lại state
Python:

from random import Random
 
class MT19937:
    def __init__(self, seed):
        self.w = 32
        self.n = 624
        self.m = 397
        self.r = 31
        self.a = 0x9908B0DF
        self.u, self.d = 11, 0xFFFFFFFF
        self.s, self.b = 7, 0x9D2C5680
        self.t, self.c = 15, 0xEFC60000
        self.l = 18
        self.f = 1812433253
        self.lower_mask = (1 << self.r) - 1  
        self.upper_mask = (~self.lower_mask) & 0xFFFFFFFF  
        self.mt = [0] * self.n 
        self.index = self.n 
        self.seed_mt(seed)
 
    def seed_mt(self, seed):
        self.mt[0] = seed & 0xFFFFFFFF
        for i in range(1, self.n):
            self.mt[i] = (self.f * (self.mt[i - 1] ^ (self.mt[i - 1] >> (self.w - 2))) + i) & 0xFFFFFFFF
 
    def extract_number(self):
        if self.index >= self.n:
            self.twist()
        y = self.mt[self.index]
        y ^= (y >> self.u) & self.d
        y ^= (y << self.s) & self.b 
        y ^= (y << self.t) & self.c 
        y ^= (y >> self.l)
        self.index += 1
        return y & 0xFFFFFFFF
 
    def twist(self):
        for i in range(self.n):
            x = (self.mt[i] & self.upper_mask) + (self.mt[(i + 1) % self.n] & self.lower_mask)
            xA = x >> 1
            if x % 2 != 0:  # lowest bit of x is 1
                xA ^= self.a
            self.mt[i] = self.mt[(i + self.m) % self.n] ^ xA
        self.index = 0

So sánh với python thì có lệch một chút:

 
rng = MT19937(548)
r1 = rng.extract_number()
real = Random(548)
r2 = real.getrandbits(32)
print(r1)
print(r2)
'''
1927303077
4100404852
'''

Bởi vì trong Python đã có sự điều chỉnh nhẹ về seed cho nên đầu ra ở trên có phần hơi khác. https://github.com/python/cpython/blob/main/Lib/random.py

Lí do cho sự khác nhau đó nằm ở cách Python xử lí seed. Python xử lí nhiều trường hợp khác nhau cho seed, bao gồm cả trường hợp seed ta nhập vào lớn hơn 32 bits trong khi đó thuật toán MT19937 ở trên thì bỏ qua bước này.

/* This algorithm relies on the number being unsigned.
 * So: if the arg is a PyLong, use its absolute value.
 * Otherwise use its hash value, cast to unsigned.
 */
if (PyLong_CheckExact(arg)) {
    n = PyNumber_Absolute(arg);
} else if (PyLong_Check(arg)) {
    /* Calling int.__abs__() prevents calling arg.__abs__(), which might
        return an invalid value. See issue #31478. */
    _randomstate *state = _randomstate_type(Py_TYPE(self));
    n = PyObject_CallOneArg(state->Long___abs__, arg);
}
else {
    Py_hash_t hash = PyObject_Hash(arg);
    if (hash == -1)
        goto Done;
    n = PyLong_FromSize_t((size_t)hash);
}
if (n == NULL)
    goto Done;
 
/* Now split n into 32-bit chunks, from the right. */
bits = _PyLong_NumBits(n);
if (bits == (size_t)-1 && PyErr_Occurred())
    goto Done;
 
/* Figure out how many 32-bit chunks this gives us. */
keyused = bits == 0 ? 1 : (bits - 1) / 32 + 1;
 
/* Convert seed to byte sequence. */
key = (uint32_t *)PyMem_Malloc((size_t)4 * keyused);
if (key == NULL) {
    PyErr_NoMemory();
    goto Done;
}
res = _PyLong_AsByteArray((PyLongObject *)n,
                            (unsigned char *)key, keyused * 4,
                            PY_LITTLE_ENDIAN,
                            0, /* unsigned */
                            1); /* with exceptions */
if (res == -1) {
    goto Done;
}
 
init_by_array(self, key, keyused);

Tóm tắt: Nếu seed của ta là một số nguyên dương thì nó sẽ chia thành các chunks có độ dài 32 bits (bất kể seed ban đầu có độ dài là bao nhiêu) để tạo ra một danh sách gồm các key. Nếu như seed là số âm thì sẽ lấy trị tuyệt đối.

>>> import random
>>> rng1 = random.Random(1234)
>>> rng2 = random.Random(-1234)
>>> r1 = rng1.getrandbits(32)
>>> r2 = rng2.getrandbits(32)
>>> print(r1 == r2)
True
>>>

Còn nếu như là số thực thì sẽ lấy hash của nó.

Initial state lúc này sẽ được sinh ra như sau:

/* initialize by an array with array-length */
/* init_key is the array for initializing keys */
/* key_length is its length */
/* initializes mt[N] with a seed */
static void
init_genrand(RandomObject *self, uint32_t s)
{
    int mti;
    uint32_t *mt;
 
    mt = self->state;
    mt[0]= s;
    for (mti=1; mti<N; mti++) {
        mt[mti] =
        (1812433253U * (mt[mti-1] ^ (mt[mti-1] >> 30)) + mti);
        /* See Knuth TAOCP Vol2. 3rd Ed. P.106 for multiplier. */
        /* In the previous versions, MSBs of the seed affect   */
        /* only MSBs of the array mt[].                                */
        /* 2002/01/09 modified by Makoto Matsumoto                     */
    }
    self->index = mti;
    return;
}
static void
init_by_array(RandomObject *self, uint32_t init_key[], size_t key_length)
{
    size_t i, j, k, l;       /* was signed in the original code. RDH 12/16/2002 */
    uint32_t *mt;
 
    mt = self->state;
    init_genrand(self, 19650218U);
    i=1; j=0;
    k = (N>key_length ? N : key_length);
 
    for (; k; k--) {
        mt[i] = (mt[i] ^ ((mt[i-1] ^ (mt[i-1] >> 30)) * 1664525U))
                 + init_key[j] + (uint32_t)j; /* non linear */
        i++; j++;
        if (i>=N) { mt[0] = mt[N-1]; i=1; }
        if (j>=key_length) j=0;
    }
 
    for (k=N-1; k; k--) {
        mt[i] = (mt[i] ^ ((mt[i-1] ^ (mt[i-1] >> 30)) * 1566083941U))
                 - (uint32_t)i; /* non linear */
        i++;
        if (i>=N) { mt[0] = mt[N-1]; i=1; }
    }
 
    mt[0] = 0x80000000U; /* MSB is 1; assuring non-zero initial array */
}

Nó bao gồm 4 bước chính như sau:

Bước 1: Tạo một state mt[] với seed là 19650218
Bước 2:
- Dùng mảng key (tức seed truyền vào, có thể dài hơn 32-bit) để cộng vào mt[].
- Nếu key ngắn hơn N thì nó được lặp lại nhiều lần cho đủ.
Bước 3: Mix state mt[]
Bước 4: Đặt lại mt[0] = 0x80000000

from random import Random
 
class MT19937:
    def __init__(self, seed):
        self.w = 32
        self.n = 624
        self.m = 397
        self.r = 31
        self.a = 0x9908B0DF
        self.u, self.d = 11, 0xFFFFFFFF
        self.s, self.b = 7, 0x9D2C5680
        self.t, self.c = 15, 0xEFC60000
        self.l = 18
        self.f = 1812433253
        self.lower_mask = (1 << self.r) - 1  
        self.upper_mask = (~self.lower_mask) & 0xFFFFFFFF  
        self.mt = [0] * self.n 
        self.index = self.n 
        self.seed_mt(seed)
 
    def seed_mt(self, seed):
        self.mt[0] = seed & 0xFFFFFFFF
        for i in range(1, self.n):
            self.mt[i] = (self.f * (self.mt[i - 1] ^ (self.mt[i - 1] >> (self.w - 2))) + i) & 0xFFFFFFFF
 
    def extract(self):
        if self.index >= self.n:
            self.twist()
        y = self.mt[self.index]
        y ^= (y >> self.u) & self.d
        y ^= (y << self.s) & self.b 
        y ^= (y << self.t) & self.c 
        y ^= (y >> self.l)
        self.index += 1
        return y & 0xFFFFFFFF
 
    def twist(self):
        for i in range(self.n):
            x = (self.mt[i] & self.upper_mask) + (self.mt[(i + 1) % self.n] & self.lower_mask)
            xA = x >> 1
            if x % 2 != 0: 
                xA ^= self.a
            self.mt[i] = self.mt[(i + self.m) % self.n] ^ xA
        self.index = 0
class PythonMT19937(MT19937):
    def __init__(self, seed):
        MT19937.__init__(self, seed)
        if seed is not None:
            self.seed(seed)
 
    def seed(self, n):
        lower = 0xffffffff
        keys = []
 
        while n:
            keys.append(n & lower)
            n >>= 32
 
        if len(keys) == 0:
            keys.append(0)
 
        self.init_by_array(keys)
 
    def init_by_array(self, keys):
        MT19937.seed_mt(self, 0x12bd6aa)
        i, j = 1, 0
        for _ in range(max(624, len(keys))):
            self.mt[i] = ((self.mt[i] ^ ((self.mt[i-1] ^
                            (self.mt[i-1] >> 30)) * 0x19660d)) + keys[j] + j) & 0xffffffff
            i += 1
            j += 1
            if i >= 624:
                self.mt[0] = self.mt[623]
                i = 1
            j %= len(keys)
 
        for _ in range(623):
            self.mt[i] = ((self.mt[i] ^ ((self.mt[i-1] ^
                            (self.mt[i-1] >> 30)) * 0x5d588b65)) - i) & 0xffffffff
            i += 1
            if i >= 624:
                self.mt[0] = self.mt[623]
                i = 1
 
        self.mt[0] = 0x80000000
 
import random
seed = 2**32-33
print(seed.bit_length())
rng1 = random.Random(seed)
rng2 = PythonMT19937(seed)
rng3 = MT19937(seed)
r1 = rng1.getrandbits(32)
r2 = rng2.extract()
assert r1 == r2

Tham khảo: https://stackered.com/blog/python-random-prediction/#pythons-seeding-procedure

Crack

Bước tampering ở trên về cơ bản là có thể đảo ngược lại được. Nên khi ta thu tập đủ output thì ta hoàn toàn có thể recover lại internal state và dự đoán được giá trị tiếp theo của hàm.

import random
def unshiftRight(x, shift):
    res = x
    for i in range(32):
        res = x ^ res >> shift
    return res
 
def unshiftLeft(x, shift, mask):
    res = x
    for i in range(32):
        res = x ^ (res << shift & mask)
    return res
 
def untemper(v):
    v = unshiftRight(v, 18)
    v = unshiftLeft(v, 15, 0xefc60000)
    v = unshiftLeft(v, 7, 0x9d2c5680)
    v = unshiftRight(v, 11)
    return v

Bash Random

Có nhiều phiên bản khác nhau cho hàm $RANDOM. Mọi người có thể kiểm tra bằng cách gõ bash --version trên terminal của mình.

duc112006@LAPTOP-VB45ARKK:~$ bash --version
GNU bash, version 5.1.16(1)-release (x86_64-pc-linux-gnu)
Copyright (C) 2020 Free Software Foundation, Inc.
License GPLv3+: GNU GPL version 3 or later <http://gnu.org/licenses/gpl.html>
 
This is free software; you are free to change and redistribute it.
There is NO WARRANTY, to the extent permitted by law.

Ở đây hàm $RANDOM đang chạy ở phiên bản 5.1 sử dụng Lehmer random number generator

Hàm intrand32() của nó như sau:

intrand32 (last)
     u_bits32_t last;
{
  /* Minimal Standard generator from
     "Random number generators: good ones are hard to find",
     Park and Miller, Communications of the ACM, vol. 31, no. 10,
     October 1988, p. 1195. Filtered through FreeBSD.
 
     x(n+1) = 16807 * x(n) mod (m).
 
     We split up the calculations to avoid overflow.
 
     h = last / q; l = x - h * q; t = a * l - h * r
     m = 2147483647, a = 16807, q = 127773, r = 2836
 
     There are lots of other combinations of constants to use; look at
     <https://www.gnu.org/software/gsl/manual/html_node/Other-random-number-generators.html#Other-random-number-generators> */
 
  bits32_t h, l, t;
  u_bits32_t ret;
 
  /* Can't seed with 0. */
  ret = (last == 0) ? 123459876 : last;
  h = ret / 127773;
  l = ret - (127773 * h);
  t = 16807 * l - 2836 * h;
  ret = (t < 0) ? t + 0x7fffffff : t;
 
  return (ret);
}
 
static u_bits32_t
genseed ()
{
  struct timeval tv;
  u_bits32_t iv;
 
  gettimeofday (&tv, NULL);
  iv = (u_bits32_t)seedrand;		/* let the compiler truncate */
  iv = tv.tv_sec ^ tv.tv_usec ^ getpid () ^ getppid () ^ current_user.uid ^ iv;
  return (iv);
}
 
#define BASH_RAND_MAX	32767		/* 0x7fff - 16 bits */
 
/* Returns a pseudo-random number between 0 and 32767. */
int
brand ()
{
  unsigned int ret;
 
  rseed = intrand32 (rseed);
  if (shell_compatibility_level > 50)
    ret = (rseed >> 16) ^ (rseed & 65535);
  else
    ret = rseed;
  return (ret & BASH_RAND_MAX);
}

Công thức cụ thể sẽ là

s_{n + 1} = a s_{n} mod m

với $a = 16807, m = 2147483647$ .

Hàm $RANDOM chỉ trả về các số nằm trong khoảng từ 0 tới 32676

BASH_RAND_MAX 32767

Đầu vào sẽ là một seed, seed sẽ được giữ nguyên giá trị hoặc chuyển thành 123459876 nếu như ban đầu ta để seed = 0.

  bits32_t h, l, t;
  u_bits32_t ret;
 
  /* Can't seed with 0. */
  ret = (last == 0) ? 123459876 : last;
  h = ret / 127773;
  l = ret - (127773 * h);
  t = 16807 * l - 2836 * h;
  ret = (t < 0) ? t + 0x7fffffff : t;
 
  return (ret);

Đối với bash phiên bản 5.0 trở lên thì sẽ trả về ret = (rseed >> 16) ^ (rseed & 65535); còn ngược lại thì giữ nguyên. Tức là output là XOR của hai nửa 16-bit, rồi chỉ giữ 15 bit thấp (0x7fff).
Để sinh seed thì ta sử dụng Schrage’s method để tránh bị tràn số. Cụ thể mọi người có thể xem tại https://en.wikipedia.org/wiki/Lehmer_random_number_generator
Implement:

import subprocess
 
BASH_RAND_MAX = 0x7fff 
 
class BashRandom:
    def __init__(self, seed: int, shell_compatibility_level: int = 51):
        self.rseed = seed & 0xffffffff
        self.shell_compat = int(shell_compatibility_level)
    @staticmethod
    def _intrand32(last: int) -> int:
        if last == 0:
            last = 123459876
        q = 127773
        r = 2836
        a = 16807
        m = 0x7fffffff  
 
        h = last // q
        l = last - (q * h)
        t = a * l - r * h
        ret = t + m if t < 0 else t
        return ret
 
    def _brand_(self) -> int:
        self.rseed = self._intrand32(self.rseed)
 
        if self.shell_compat > 50:
            v = ((self.rseed >> 16) ^ (self.rseed & 0xffff))
        else:
            v = self.rseed
 
        return v & BASH_RAND_MAX
    def next(self) -> int:
        return self._brand_()
    def next_n(self, n: int) -> list:
        return [self._brand_() for _ in range(n)]
# GNU bash, version 5.1.16
def bash_random(seed):
    if seed is None:
        cmd = ["bash", "-c", "echo $RANDOM"]
    else:
        cmd = ["bash", "-c", f"RANDOM={int(seed)}; echo $RANDOM"]
    proc = subprocess.run(["bash", "-c", cmd], capture_output=True, text=True, check=True)
    return int(proc.stdout.strip())
def bash_random_n(seed, count):
    if count < 1:
        return []
    if seed is None:
        cmd = f"for i in $(seq {count}); doecho $RANDOM; done"
    else:
        cmd = f"RANDOM={int(seed)}; for i in $(seq {count}); do echo $RANDOM; done"
    proc = subprocess.run(["bash", "-c", cmd], capture_output=True, text=True, check=True)
    lines = [ln for ln in proc.stdout.splitlines() if ln.strip() != ""]
    return [int(x) for x in lines]
print(bash_random_n(seed = 1337, count = 10))
rng = BashRandom(seed= 1337, shell_compatibility_level=51)
print(rng.next_n(10))
'''
[24697, 15233, 8710, 4659, 20253, 16480, 30033, 24872, 17510, 11420]
[24697, 15233, 8710, 4659, 20253, 16480, 30033, 24872, 17510, 11420]
'''

Cracking

Ý tưởng crack cho phiên bản 5.0 trở lên.
Ta biết rằng trước khi output ra kết quả của hàm rand thì giá trị của nó được thay đổi bằng cách XOR 2 nửa 16 bit rồi sau đó chỉ giữ lại 15 bit thấp ( MSB bit bị khuyết thông tin).
Như vậy ta sẽ có

M = 0x7fffffff
A = 16807
MASK15 = 0x7fff
 
def _map(x):
    return (((x >> 16) ^ (x & 0xffff)) & MASK15)
 
def recover_bash_seed(outputs):
    if not outputs:
        return []
    v0 = outputs[0] & MASK15
    cand = []
    for y in (v0, v0 | 0x8000):
        for high in range(1 << 15):
            low = high ^ y
            x = (high << 16) | low
            cand.append(x)
    invA = pow(A, -1, M)
    good = []
    for x0 in cand:
        x = x0
        ok = True
        for v in outputs:
            if _map(x) != (v & MASK15):
                ok = False
                break
            x = (A * x) % M
        if ok:
            seed = (invA * x0) % M
            good.append(seed)
    return sorted(set(good))
 
if __name__ == "__main__":
    outs = [5154, 3081, 27973]
    seeds = recover_bash_seed(outs)
    print(seeds)

C Random

Tham khảo tại:
https://www.mscs.dal.ca/~selinger/random/
https://stackoverflow.com/questions/18969783/how-can-i-get-the-sourcecode-for-rand-c
Thuật toán hoạt động như sau:
Với một seed $s$ và mảng $r_{0}, r_{1}, ..., r_{33}$ , số được sinh ra sẽ thỏa:

$r_{0} = s$
$r_{i} = (16807 \times (signed int) r_{i - 1}) mod 2147483647, \forall i = 1, .., 30$
$r_{i} = r_{i - 31}, i = 31, 32, 33$
Từ $r = 34$ trở đi thì thuật toán sẽ trở thành
$r_{i} = (r_{i - 3} + r_{i - 31}) mod 4294967296 (i \geq 34)$
Kết quả thứ i của hàm rand() sẽ là $r_{i} + 344 >> 1$
Implement:

M31 = 2147483647  
M32 = 2**32     
def to_int32_signed(x: int) -> int:
    x &= 0xFFFFFFFF
    if x & 0x80000000:
        return x - 0x100000000
    return x
 
class GlibcRandom:
    def __init__(self, seed: int):
 
        r = [0] * 344
        r[0] = seed & 0xFFFFFFFF
        for i in range(1, 31):
            prev_signed = to_int32_signed(r[i-1])
            r[i] = (16807 * prev_signed) % M31
            if r[i] < 0:
                r[i] += M31 
        for i in range(31, 34):
            r[i] = r[i-31]
        for i in range(34, 344):
            r[i] = (r[i-31] + r[i-3]) & 0xFFFFFFFF
 
        self.r = r  
    
    def random(self) -> int:
        val = (self.r[-31] + self.r[-3]) & 0xFFFFFFFF
        self.r.append(val)
        return (val >> 1) & 0x7FFFFFFF  
    def next_many(self, n: int):
        return [self.random() for _ in range(n)]
 
check = [
    1804289383, 846930886, 1681692777, 1714636915, 1957747793, 424238335,
    719885386, 1649760492, 596516649, 1189641421, 1025202362, 1350490027,
    783368690, 1102520059, 2044897763, 1967513926, 1365180540, 1540383426,
    304089172, 1303455736, 35005211, 521595368, 294702567, 1726956429,
    336465782, 861021530, 278722862, 233665123, 2145174067, 468703135,
    1101513929, 1801979802, 1315634022, 635723058, 1369133069, 1125898167,
    1059961393, 2089018456, 628175011, 1656478042, 1131176229, 1653377373,
    859484421, 1914544919, 608413784, 756898537, 1734575198, 1973594324,
    149798315, 2038664370, 1129566413, 184803526, 412776091, 1424268980,
    1911759956, 749241873, 137806862, 42999170, 982906996, 135497281
]
rng = GlibcRandom(seed=1)
generated = rng.next_many(60)
test = (generated == check)
print(test)

Cracking

Như ta quan sát thấy thì kể từ phần tử thứ $i \geq 34$ trở đi thì được tính bởi một công thức tuyến tính state[i] = state[i - 3] + state[i - 31] đồng thời kết quả trả về bị mất đi một bit cuối cho nên mỗi output sẽ có 2 khả năng khác nhau cho bit cuối này.

Nếu ta biết được 2 trong số 3 giá trị trong ràng buộc tuyến tính ở trên thì ta hoàn toàn có thể tính lại được giá trị còn lại.

JS Random

Tham khảo:

https://developer.mozilla.org/en-US/docs/Web/JavaScript/Reference/Global_Objects/Math/random
https://v8.dev/blog/math-random

https://chromium.googlesource.com/v8/v8/+/refs/heads/master/src/numbers/math-random.cc

https://denolib.github.io/v8-docs/random-number-generator_8h_source.html

https://github.com/v8/v8/blob/12.5.66/src/base/utils/random-number-generator.h#L111

Hàm Math.random() trong JS trả về một số thực dương nằm trong khoảng $[0, 1)$ .

// Copyright 2018 the V8 project authors. All rights reserved.
// Use of this source code is governed by a BSD-style license that can be
// found in the LICENSE file.
#include "src/numbers/math-random.h"
#include "src/base/utils/random-number-generator.h"
#include "src/common/assert-scope.h"
#include "src/execution/isolate.h"
#include "src/objects/contexts-inl.h"
#include "src/objects/fixed-array.h"
#include "src/objects/smi.h"
namespace v8 {
namespace internal {
void MathRandom::InitializeContext(Isolate* isolate,
                                   DirectHandle<Context> native_context) {
  auto cache = Cast<FixedDoubleArray>(
      isolate->factory()->NewFixedDoubleArray(kCacheSize));
  for (int i = 0; i < kCacheSize; i++) cache->set(i, 0);
  native_context->set_math_random_cache(*cache);
  DirectHandle<PodArray<State>> pod =
      PodArray<State>::New(isolate, 1, AllocationType::kOld);
  native_context->set_math_random_state(*pod);
  ResetContext(*native_context);
}
void MathRandom::ResetContext(Tagged<Context> native_context) {
  native_context->set_math_random_index(Smi::zero());
  State state = {0, 0};
  Cast<PodArray<State>>(native_context->math_random_state())->set(0, state);
}
Address MathRandom::RefillCache(Isolate* isolate, Address raw_native_context) {
  Tagged<Context> native_context =
      Cast<Context>(Tagged<Object>(raw_native_context));
  DisallowGarbageCollection no_gc;
  Tagged<PodArray<State>> pod =
      Cast<PodArray<State>>(native_context->math_random_state());
  State state = pod->get(0);
  // Initialize state if not yet initialized. If a fixed random seed was
  // requested, use it to reset our state the first time a script asks for
  // random numbers in this context. This ensures the script sees a consistent
  // sequence.
  if (state.s0 == 0 && state.s1 == 0) {
    uint64_t seed;
    if (v8_flags.random_seed != 0) {
      seed = v8_flags.random_seed;
    } else {
      isolate->random_number_generator()->NextBytes(&seed, sizeof(seed));
    }
    state.s0 = base::RandomNumberGenerator::MurmurHash3(seed);
    state.s1 = base::RandomNumberGenerator::MurmurHash3(~seed);
    CHECK(state.s0 != 0 || state.s1 != 0);
  }
  Tagged<FixedDoubleArray> cache =
      Cast<FixedDoubleArray>(native_context->math_random_cache());
  // Create random numbers.
  for (int i = 0; i < kCacheSize; i++) {
    // Generate random numbers using xorshift128+.
    base::RandomNumberGenerator::XorShift128(&state.s0, &state.s1);
    cache->set(i, base::RandomNumberGenerator::ToDouble(state.s0));
  }
  pod->set(0, state);
  Tagged<Smi> new_index = Smi::FromInt(kCacheSize);
  native_context->set_math_random_index(new_index);
  return new_index.ptr();
}
}  // namespace internal
}  // namespace v8

Trong engine v8, Math.random() sẽ sử dụng một PRNG là xorshift128

for (int i = 0; i < kCacheSize; i++) {
    // Generate random numbers using xorshift128+.
    base::RandomNumberGenerator::XorShift128(&state.s0, &state.s1);
    cache->set(i, base::RandomNumberGenerator::ToDouble(state.s0));
  }
  pod->set(0, state);

Cụ thể như sau:

   static inline void XorShift128(uint64_t* state0, uint64_t* state1) {
     uint64_t s1 = *state0;
     uint64_t s0 = *state1;
     *state0 = s0;
     s1 ^= s1 << 23;
     s1 ^= s1 >> 17;
     s1 ^= s0;
     s1 ^= s0 >> 26;
     *state1 = s1;
   }
 
   static uint64_t MurmurHash3(uint64_t);
 
  private:
   static const int64_t kMultiplier = V8_2PART_UINT64_C(0x5, deece66d);
   static const int64_t kAddend = 0xb;
   static const int64_t kMask = V8_2PART_UINT64_C(0xffff, ffffffff);
 
   int Next(int bits) V8_WARN_UNUSED_RESULT;
 
   int64_t initial_seed_;
   uint64_t state0_;
   uint64_t state1_;
 };
 
 }  // namespace base
 }  // namespace v8
 
 #endif  // V8_BASE_UTILS_RANDOM_NUMBER_GENERATOR_H_

PRNG giữ hai trạng thái 64 bit là state0 và state1 sau đó thực hiện biến đổi 2 state thông qua các phép dịch bit và XOR. Kết quả sau khi chạy là một cặp giá trị (state0,state1)

Trong JS có khai báo trước các giá trị như sau

  static const int kCacheSize = 64;
  static const int kStateSize = 2 * kInt64Size;

kCacheSize là kích thước của bộ đệm mà V8 dùng để giữ sẵn các số ngẫu nhiên đã sinh ra, thay vì mỗi lần gọi Math.random() thì phải chạy trực tiếp XorShift128.

Khi cache hết, V8 dùng XorShift128 để sinh thêm 64 số mới, rồi lưu vào cache. Ở đây mảng chứa cache được lấy từ cuối tới đầu.

// random-number-generator.cc
double RandomNumberGenerator::Next() {
  if (index_ == 0) RefillCache();
  return buffer_[--index_];
}

buffer_ là mảng chứa cache (kCacheSize = 64). Ban đầu con trỏ index_ được đặt bằng 0. Sau khi refill sẽ là 64.

Tiếp theo các số nguyên 64 bit được chuyển sang các số thực trong $[0, 1)$ với các bước như sau:

Đầu tiên lấy 52 bit cao của output - mantissa = output >> 12 rồi sau đó ghép với số mũ 0x3ff0000000000000 ( bằng toán tử | ).

Theo format IEEE-754 thì một số double có dạng như sau:

sign (1 bit) | exponent (11 bit) | mantissa (52 bit)

V8 sẽ không sử dụng hết 64 bit mà chỉ giữ lại 52 bit cao. Số mũ 0x3ff đúng bằng 1023.

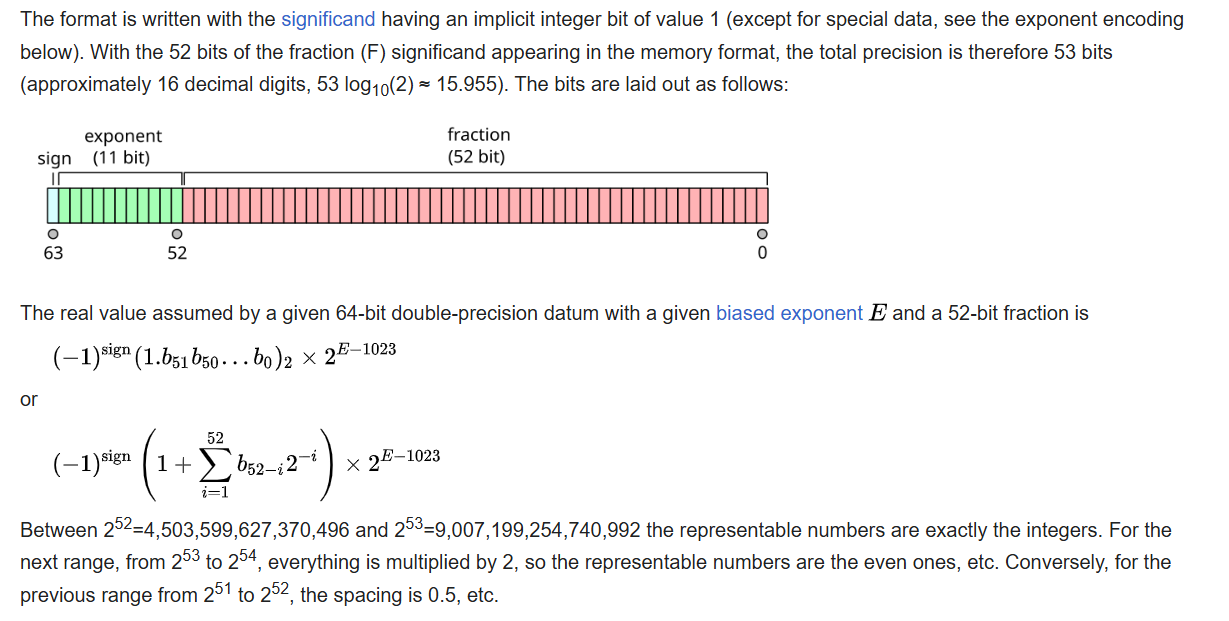
Việc nhân với số mũ như vậy giúp đưa số về trong khoảng [1.0,2.0) sau đó trừ đi 1 để thu lại kết quả của hàm random.

Cracking

Khi gọi hàm random thì các số được trả về theo kiểu LIFO nên ta cần đảo ngược dãy thu được trước khi tiến hành crack. Sau đó phần còn lại ta sẽ để cho Z3 xử lí, bằng cách mô phỏng lại ràng buộc giữa state0 và state1 thông qua các phép dịch trái, dịch phải, và XOR.

#!/usr/bin/python3
import z3
import struct
import sys
 
""" 
Solving for seed states in XorShift128+ used in V8
> <https://v8.dev/blog/math-random>
> <https://apechkurov.medium.com/v8-deep-dives-random-thoughts-on-math-random-fb155075e9e5>
> <https://blog.securityevaluators.com/hacking-the-javascript-lottery-80cc437e3b7f>
 
> Tested on Chrome(102.0.5005.61) or Nodejs(v18.2.0.) 
"""
 
"""
Plug in a handful random number sequences from node/chrome
> Array.from(Array(5), Math.random)
 
(Optional) In node, we can specify the seed
> node --random_seed=1337
"""
sequence = [
  0.9311600617849973,
  0.3551442693830502,
  0.7923158995678377,
  0.787777942408997,
  0.376372264303491,
  # 0.23137147109312428
]
 
"""
Random numbers generated from xorshift128+ is used to fill an internal entropy pool of size 64
> <https://github.com/v8/v8/blob/7a4a6cc6a85650ee91344d0dbd2c53a8fa8dce04/src/numbers/math-random.cc#L35>
 
Numbers are popped out in LIFO(Last-In First-Out) manner, hence the numbers presented from the entropy pool are reveresed.
"""
sequence = sequence[::-1]
 
solver = z3.Solver()
 
"""
Create 64 bit states, BitVec (uint64_t)
> static inline void XorShift128(uint64_t* state0, uint64_t* state1);
> <https://github.com/v8/v8/blob/a9f802859bc31e57037b7c293ce8008542ca03d8/src/base/utils/random-number-generator.h#L119>
"""
se_state0, se_state1 = z3.BitVecs("se_state0 se_state1", 64)
 
for i in range(len(sequence)):
    """
    XorShift128+
    > <https://vigna.di.unimi.it/ftp/papers/xorshiftplus.pdf>
    > <https://github.com/v8/v8/blob/a9f802859bc31e57037b7c293ce8008542ca03d8/src/base/utils/random-number-generator.h#L119>
 
    class V8_BASE_EXPORT RandomNumberGenerator final {
        ...
        static inline void XorShift128(uint64_t* state0, uint64_t* state1) {
            uint64_t s1 = *state0;
            uint64_t s0 = *state1;
            *state0 = s0;
            s1 ^= s1 << 23;
            s1 ^= s1 >> 17;
            s1 ^= s0;
            s1 ^= s0 >> 26;
            *state1 = s1;
        }
        ...
    }
    """
    se_s1 = se_state0
    se_s0 = se_state1
    se_state0 = se_s0
    se_s1 ^= se_s1 << 23
    se_s1 ^= z3.LShR(se_s1, 17)  # Logical shift instead of Arthmetric shift
    se_s1 ^= se_s0
    se_s1 ^= z3.LShR(se_s0, 26)
    se_state1 = se_s1
 
    """
    IEEE 754 double-precision binary floating-point format
    > <https://en.wikipedia.org/wiki/Double-precision_floating-point_format>
    > <https://www.youtube.com/watch?v=p8u_k2LIZyo&t=257s>
 
    Sign (1)    Exponent (11)    Mantissa (52)
    [#]         [###########]    [####################################################]
    """
 
    """
    Pack as `double` and re-interpret as unsigned `long long` (little endian)
    > <https://stackoverflow.com/a/65377273>
    """
    float_64 = struct.pack("d", sequence[i] + 1)
    u_long_long_64 = struct.unpack("<Q", float_64)[0]
 
    """
    # visualize sign, exponent & mantissa
    bits = bin(u_long_long_64)[2:]
    bits = '0' * (64-len(bits)) + bits
    print(f'{bits[0]} {bits[1:12]} {bits[12:]}')
    """
 
    # Get the lower 52 bits (mantissa)
    mantissa = u_long_long_64 & ((1 << 52) - 1)
 
    # Compare Mantissas
    solver.add(int(mantissa) == z3.LShR(se_state0, 12))
 
if solver.check() == z3.sat:
    model = solver.model()
 
    states = {}
    for state in model.decls():
        states[state.__str__()] = model[state]
 
    print(states)
 
    state0 = states["se_state0"].as_long()
 
    """
    Extract mantissa
    - Add `1.0` (+ 0x3FF0000000000000) to 52 bits
    - Get the double and Subtract `1` to obtain the random number between [0, 1)
 
    > <https://github.com/v8/v8/blob/a9f802859bc31e57037b7c293ce8008542ca03d8/src/base/utils/random-number-generator.h#L111>
 
    static inline double ToDouble(uint64_t state0) {
        // Exponent for double values for [1.0 .. 2.0)
        static const uint64_t kExponentBits = uint64_t{0x3FF0000000000000};
        uint64_t random = (state0 >> 12) | kExponentBits;
        return base::bit_cast<double>(random) - 1;
    }
    """
    u_long_long_64 = (state0 >> 12) | 0x3FF0000000000000
    float_64 = struct.pack("<Q", u_long_long_64)
    next_sequence = struct.unpack("d", float_64)[0]
    next_sequence -= 1
 
    print(next_sequence)

Go Random

Tham khảo:

https://cs.opensource.google/go/go/+/refs/tags/go1.24.2:src/math/rand/rand.go

https://go.dev/src/math/rand/rng.go

https://appliedgo.net/random/

Hàm math/rand sinh số ngẫu nhiên trong Golang sử dụng một thuật toán gọi là Additive Lagged Fibonacci Generator

// from rng.go - (c) the Go team
 
type rngSource struct {
	tap  int         // index into vec
	feed int         // index into vec
	vec  [_LEN]int64 // current feedback register
}
 
func (rng *rngSource) Int63() int64 {
	rng.tap--
	if rng.tap < 0 {
		rng.tap += _LEN
	}
 
	rng.feed--
	if rng.feed < 0 {
		rng.feed += _LEN
	}
 
	x := (rng.vec[rng.feed] + rng.vec[rng.tap]) & _MASK
	rng.vec[rng.feed] = x
	return x
}

Thuật toán gồm các thành phần như sau:
Đầu tiên là các hằng số

const (
	rngLen   = 607
	rngTap   = 273
	rngMax   = 1 << 63
	rngMask  = rngMax - 1
	int32max = (1 << 31) - 1
)

rngLen = 607: độ dài thanh ghi vòng (ring buffer) – số phần tử trạng thái.
rngTap = 273: khoảng “tap” – khoảng cách giữa 2 chỉ số dùng cộng.
rngMax = 1<<63, rngMask = rngMax-1: dùng để cắt về 63-bit không âm khi trả Int63.
int32max = 2^31 - 1: mô-đun của bộ sinh Lehmer dùng lúc seed.
rngCooked[607]: bảng hằng 607 số 64-bit, dùng trộn khi khởi tạo trạng thái (seeding) để tránh trạng thái yếu.

type rngSource struct {
    tap  int           // con trỏ tap
    feed int           // con trỏ feed
    vec  [rngLen]int64 // mảng trạng thái, độ dài 607
}

tap và feed là hai con trỏ giảm dần chạy vòng quanh mảng trạng thái và vec là một vector có độ dài là 607 để lưu toàn bộ trạng thái hiện tại.

def seedrand(x):
    A = 48271
    Q = 44488
    R = 3399
    hi = x // Q
    lo = x % Q
    x = A * lo - R * hi
    if x < 0:
        x += INT32_MAX
    return x

Hàm seedrand(x) sử dụng thuật toán Park-Miller LCG để tính toán các giá trị tiếp theo của seed. Mục đích của việc gọi hàm này để làm nhiễu trạng thái đầu ra của vec

Tiếp theo ta có hàm seed

func (rng *rngSource) Seed(seed int64) {
	rng.tap = 0
	rng.feed = rngLen - rngTap
 
	seed = seed % int32max
	if seed < 0 {
		seed += int32max
	}
	if seed == 0 {
		seed = 89482311
	}
 
	x := int32(seed)
	for i := -20; i < rngLen; i++ {
		x = seedrand(x)
		if i >= 0 {
			var u int64
			u = int64(x) << 40
			x = seedrand(x)
			u ^= int64(x) << 20
			x = seedrand(x)
			u ^= int64(x)
			u ^= rngCooked[i]
			rng.vec[i] = u
		}
	}
}

Hàm này nhận giá trị đầu vào là seed của ta. Đặt lại hai con trỏ rng.tap=0 và rng.feed=607-273=334 tức là hai con trỏ cách nhau 334 bước trên vòng.

Chuẩn hóa seed về một số nằm trong khoảng [1,2^31-2] . Trường hợp nếu như seed == 0 thì ta lấy seed = 89482311. Tiếp theo ta sẽ làm đầy vec như sau:

Đặt x:=int32(seed)

Chạy vòng lặp từ -20 tới 606, tính x=seedrand(x) . Kể từ các vòng lặp thứ i > 0 trở đi thì ta sẽ tính. Mục đích của 20 vòng lặp đầu tiên là để làm nhiễu giá trị đầu ra của LCG tránh các mẫu lặp lại. Tiếp theo:

						if i >= 0:
                u = (_to_u64(x) << 40) & MASK64
                x = seedrand(x)
                u ^= (_to_u64(x) << 20) & MASK64
                x = seedrand(x)
                u ^= _to_u64(x)
                cooked = RNG_COOKED[i] & MASK64
                u ^= cooked
                self.vec[i] = _to_s64(u)

Nó sẽ sinh ra 3 giá trị liên tiếp bằng seedrand(x) rồi ghép chúng lại để tạo thành một số mới. Sau đó nó sẽ XOR với một hằng số cho trước là RNG_COOKED[i].

Khi chạy hết vòng lặp và có được đầy đủ các giá trị trong vec thì ta sẽ sinh ra một số 64 bit như sau:

    def uint64(self):
        self.tap -= 1
        if self.tap < 0:
            self.tap += RNG_LEN
        self.feed -= 1
        if self.feed < 0:
            self.feed += RNG_LEN
        s = (_to_u64(self.vec[self.feed]) + _to_u64(self.vec[self.tap])) & MASK64
        self.vec[self.feed] = _to_s64(s)
        return s

Mỗi lần sẽ tính self.tap-- và self.feed-- sau đó thực hiện cộng s = vec[feed] + vec[tap] và thực hiện ghi đè vec[feed]=s để sinh các phần tử mới khác.

Có hai lựa chọn sinh số ngẫu nhiên đó là uint64, trả về một số random 64 bit hoặc int63 trả về một số 63 bit.
Implement:

from rng_cooked import rng_cooked
# const: 
rngLen = 607
rngTap = 273
rngMax = 1 << 63
rngMask = rngMax - 1
int32max = (1 << 31) - 1
 
def seedrand(x):
    A = 48271
    Q = 44488
    R = 3399
    hi = x  // Q
    lo = x % Q
    x = A*lo - R*hi
    if x < 0:
        x += int32max
    return x
class RNGSource:
    def __init__(self):
        self.tap = 0 
        self.feed = rngLen - rngTap
        self.vec = [0] * rngLen
    def seed(self,seed):
        self.tap = 0 
        self.feed = rngLen - rngTap
        
        seed = seed % int32max
        if seed < 0:
            seed += int32max
        if seed == 0:
            seed = 89482311
        x = int(seed)
        for i in range(-20,rngLen):
            x = seedrand(x)
            if i >=0 :
                u = (int(x) << 40) & 0xFFFFFFFFFFFFFFFF
                x = seedrand(x)
                u ^= (int(x) << 20) & 0xFFFFFFFFFFFFFFFF
                x = seedrand(x)
                u ^= (int(x) & 0xFFFFFFFFFFFFFFFF)
                u ^= rng_cooked[i]
                self.vec[i] = u
    def int63(self):
        return self.uint64() & rngMask
    def uint64(self):
        self.tap -= 1
        if self.tap < 0:
            self.tap += rngLen
        self.feed -= 1
        if self.feed < 0:
            self.feed += rngLen
        x = self.vec[self.feed] + self.vec[self.tap]
        self.vec[self.feed] = x
        return int(x) & 0xFFFFFFFFFFFFFFFF
rng = RNGSource()
rng.seed(1234)
output = [rng.uint64() for _ in range(123)]
print(output)

Cracking

Ở mỗi bước nó sẽ trả về x = vec[feed] + vec[tap] rồi lưu lại vec[feed] = x . Về cơ bản thì đây là một hệ phương trình tuyến tính trên các biến là các giá trị ban đầu của mảng vec. Việc ta cần làm là tìm cách symbolic 607 output liên tiếp từ hàm RNG rồi mô phỏng lại quá trình tính toán seed để tạo các ràng buộc tuyến tính giữa chúng.

Đầu tiên ta symbolic lại 607 phần tử đầu tiên như sau:

from implement import *
from z3 import *
s = Solver()
vec = [BitVec(f'v_{i}', 64) for i in range(rngLen)]

Sau đó mình sẽ tạo một mảng mới cur = vec[:]. Lí do cần phải làm như vậy để khi ta mô phỏng lại các bước của thuật toán random thì các giá trị x trong vec không bị ghi đè logic.

Chẳng hạn ta có bước thay thế vec[feed] = x , ở đây x đóng vai trò vừa là biến giá trị vừa là biến ràng buộc nên sẽ không phù hợp. Ta có thể làm như sau:

cur = vec[:]
tap = 0 
feed = rngLen - rngTap
known = [rng_real.uint64() for _ in range(test_case)]
for i in range(test_case):
	tap = tap - 1 if tap >= 0 else tap - 1 + rngLen
	feed = feed - 1 if feed >=0 else feed - 1 + rngLen
	x = (cur[feed] + cur[tap]) & ((1<<64) - 1)
	s.add(x == known[i]) # buoc symbolic
	...

Sau khi đưa vào z3 chạy, nếu có nghiệm thì ta cập nhật lại vector khởi tạo mới bằng kết quả vừa giải được và chạy thêm đủ các bước trong test cases để đưa về lại trạng thái trùng với RNG ban đầu.

from implement import *
from z3 import *
 
s = Solver()
vec = [BitVec(f'v_{i}', 64) for i in range(rngLen)]
cur = vec[:]
test_case = 650
 
tap = 0
feed = rngLen - rngTap
rng_real = RNGSource(v=None)
rng_real.seed(1234)
known = [rng_real.uint64() for _ in range(test_case)]
 
for i in range(test_case):
    tap = tap - 1 if tap - 1 >=0 else tap - 1 + rngLen
    feed = feed - 1 if feed - 1 >=0 else feed - 1 + rngLen
    x = (cur[feed] + cur[tap]) & ((1<<64) - 1)
    s.add(x == known[i])
    new_cur = cur[:]
    new_cur[feed] = x
    cur = new_cur
    
 
if s.check() == sat:
    m = s.model()
    arr = [m.evaluate(vec[i]).as_long() for i in range(rngLen)]
 
    rng_test = RNGSource(v=arr)
    for _ in range(test_case):
        rng_test.uint64()
    print("Test")
    for _ in range(10):
        print(rng_real.uint64(), rng_test.uint64())
else:
    print("unsat")

Crypto and Math

Trong bài này

Crack Random

Python

Mersenne Twister MT19937

Crack

Bash Random

Cracking

C Random

Cracking

JS Random

Cracking

Go Random

Cracking

Biểu Đồ

Bảng Nội Dung