Cơ bản về lí thuyết Galois
Bài này sẽ tổng hợp những kiến thức căn bản cần biết về Galois Theory cũng như đại số trừu tượng.
Nhóm
Nhóm con chuẩn tắc
Định nghĩa 1: Giả sử $H$ là một nhóm con của một nhóm $G$. Khi đó, tập $aH = \lbrace ah | h \in H \rbrace $ được gọi là một lớp ghép trái của $H$ trong $G$. Tương tự $Ha = \lbrace ha | h \in H \rbrace $ được gọi là một lớp ghép phải của $H$ trong $G$.
Các mở rộng trường
Đặc số của vành và trường hữu hạn
Định nghĩa 1: Cho vành $A$ là một vành có đơn vị $1$. Khi đó $A$ được gọi là vành có đặc số $0$ nếu $m1 \neq 0$ với mọi số nguyên dương $m$. Ngược lại $A$ được gọi là vành có đặc số $n$ nếu $n$ là số nguyên dương nhỏ nhất là $n1=0$. Đặc số của vành được kí hiệu là $char(A)$.
Mệnh đề: Nếu $F$ là một miền nguyên thì hoặc $char(F) = 0$ hoặc $char(F) = p$, với $p$ là số nguyên tố.
Ở đây, miền nguyên là một vành giao hoán có đơn vị $1 \neq 0$ và không có ước số của $0$ khác $0$.Như vậy nếu như $n$ là đặc số của $F$ thì $n$ không thể chia viết được dưới dạng hai số nguyên dương $a,b$ phân biệt sao cho $n=ab$. Nếu không thì ta sẽ có $a1=0$ hoặc $b1=0$, mâu thuẫn với giả thiết về tính nhỏ nhất của $n$.
Như vậy ta cũng suy ra được, nếu $F$ là một vành có đơn vị và $char(F)=n>0$ thì $m1=0$ nếu và chỉ nếu $n$ là ước của $m$.
Hệ quả:
- Mọi trường có đặc số $0$ đều chứa một bản sao của trường $\mathbb{Q}$ các số hữu tỉ và đều là trường vô hạn
- Mọi miền nguyên có đặc số nguyên tố $p$ đều chứa một trường con đẳng cấu với $\mathbb{Z}_p$
Định lí. CHo $K$ là một trường hữu hạn có đặc số nguyên tố $p$. Khi đó:
- Cấp của $K$ là $p^n$ với $n$ là số chiều của không gian vector $K$ trên $\mathbb{Z}_p$
- Phương trình $x^{p^n}-x=0$ có $p^n$ nghiệm phân biệt trong $K$.
- $\displaystyle x^{p^{n}}-x = x \prod_{u_{i}\in K}(x-u_{i}), K^{*} \in K \setminus \lbrace 0 \rbrace$
Mở rộng bậc hữu hạn
Định nghĩa 2: Cho $F$ và $K$ là hai trường. Trường $F$ được gọi là một mở rộng của $K$ nếu $K$ là một vành con của $F$.
Ví dụ:
$\mathbb{R} \subset \mathbb{C}$ có nghĩa là mọi phần tử của $\mathbb{R}$ đều thuộc $\mathbb{C}$ và các phép toán trong $\mathbb{R}$ là các phép toán trong $\mathbb{C}$ khi ta xét các phần tử của $\mathbb{R}$ như các phần tử của $\mathbb{C}$.Hơn nữa, phần tử đơn vị $0$ của phép cộng và phần tử đơn vị $1$ của phép nhân trong $\mathbb{R}$ cũng chính là các phần tử đơn vị trong $\mathbb{C}$.
Tiếp theo, nếu trường $F$ là một mở rộng của trường $K$ thì dễ chỉ ra rằng $F$ là một không gian vector trên $K$. Số chiều của không gian vector này được gọi là bậc mở rộng của $F$ trên $K$ và được kí hiệu là $[F:K]$. Trường $F$ được gọi là mở rộng bậc hữu hạn hoặc vô hạn của $K$ nếu như bậc mở rộng của nó trên $K$ là hữu hạn hoặc vô hạn.
Một tháp các trường là một dãy các trường $K_1,K_2,…,K_n$ sao cho $K_i$ là một mở rộng của $K_{i-1}$ với mọi $i = 2,3,…,n$. Khi đó ta kí hiệu tháp các trường này là:
Ví dụ: $[\mathbb{C}:\mathbb{R}] = 2$ vì $\lbrace 1,i \rbrace$ là một cơ sở của không gian vector $\mathbb{C}$ trên $\mathbb{R}$. Mọi phần tử $z \in \mathbb{C}$ đều viết được dưới dạng $z = a1 + bi$ với $a,b \in \mathbb{R}$.
Định lí Cho một tháp các trường $K \subset E \subset F$. Khi đó, $F$ là một mở rộng bậc hữu hạn của $K$ nếu và chỉ nếu $F$ là một mở rộng bậc hữu hạn của $E$ và $E$ là một mở rộng bậc hữu hạn của $K$. Hơn nữa, khi đó ta có: $[F:K] = [F:E][E:K]$.
Ví dụ: Xét tháp các trường $\mathbb{Q} \subset \mathbb{Q}(\sqrt{2}) \subset \mathbb{Q}(\sqrt{2},\sqrt{3})$. Ta có $[\mathbb{Q}(\sqrt{2}):\mathbb{Q}] = 2$ vì cơ sở của không gian vector $\mathbb{Q}(\sqrt{2})$ trên $\mathbb{Q}$ là $\lbrace 1,\sqrt{2} \rbrace$. Tương tự, $[\mathbb{Q}(\sqrt{2},\sqrt{3}):\mathbb{Q}(\sqrt{2})] = 2$ vì cơ sở của không gian vector $\mathbb{Q}(\sqrt{2},\sqrt{3})$ trên $\mathbb{Q}(\sqrt{2})$ là $\lbrace 1,\sqrt{3} \rbrace$. Do đó, theo định lí trên ta có:
Cho $F$ là một trường, và $X \subset F$. Khi đó giao của tất cả các trường con của $F$ chứa $X$ được gọi là trường con của $F$ sinh bởi $X$. Nếu $F$ là một mở rộng của $K$ và $X \subset F$ thì trường con sinh bởi $X \cup K$ được gọi là trường con sinh bởi $X$ trên $K$ và được kí hiệu là $K(X)$.
Định lí: Cho $F$ là một mở rộng của $K$ và $X \subset F$. Khi đó trường $K(X)$ gồm tất cả các phần tử có dạng:
trong đó $u_i,v_j \in X, g(v_1,v_2,…,v_m) \neq 0$ và $f,g$ là các đa thức với hệ số trong $K$.
Ví dụ: Xét mở rộng trường $\mathbb{Q}(\sqrt{2},\sqrt{3})$ trên $\mathbb{Q}$. Ta có $\mathbb{Q}(\sqrt{2},\sqrt{3}) = \mathbb{Q}(\lbrace \sqrt{2},\sqrt{3} \rbrace)$. Theo định lí trên, mọi phần tử trong $\mathbb{Q}(\sqrt{2},\sqrt{3})$ đều có dạng:
trong đó $g(\sqrt{2},\sqrt{3}) \neq 0$ và $f,g$ là các đa thức với hệ số trong $\mathbb{Q}$.
Một số bài tập:
Bài tập: Chứng minh các tập sau là các trường con của trường số phức. Hãy tìm một cơ sở và bậc mở rộng của chúng trên $\mathbb{Q}$.
a) $\mathbb{Q}[\sqrt{2}]= \lbrace a + b\sqrt{2} | a,b \in \mathbb{Q} \rbrace $
b) $\mathbb{Q}[\sqrt{p}] = \lbrace a + b\sqrt{p} | a,b \in \mathbb{Q} \rbrace $ với $p$ là số nguyên tố.
c) $\mathbb{Q}[i] = \lbrace a + bi | a,b \in \mathbb{Q} \rbrace $
d) $\mathbb{Q}[\sqrt[3]{2}] = \lbrace a + b\sqrt[3]{2} + c\sqrt[3]{4}| a,b,c \in \mathbb{Q} \rbrace $
Giải: Để chứng minh một trường là trường con của $\mathbb{C}$ ta cần chỉ ra nó khác rỗng, đồng thời thỏa mãn tính chất đóng đối với phép cộng và nhân.
Đầu tiên ta thấy các tập trên đều chứa $0$ cho nên chúng khác rỗng
a) Với mọi $x,y \in \mathbb{Q}[\sqrt{2}]$ ta có $x=a+b\sqrt{2}$, $y=c+d\sqrt{2}$ với $a,b,c,d\in \mathbb{Q}$. Khi đó:
Mặt khác vì $\displaystyle \sqrt{2}$ là số vô tỉ cho nên $\displaystyle y=0$ tương đương với $\displaystyle c=d=0$. Thật vậy, giả sử tồn tại $\displaystyle c,d\in \mathbb{Q}$ sao cho $\displaystyle y=c+d\sqrt{2} =0$ thì khi đó $\displaystyle \frac{-c}{d} =\sqrt{2}$ là vô lí vì $\displaystyle \sqrt{2}$ là số vô tỉ. Khi đó xét
Vậy $\mathbb{Q}[\sqrt{2}]$ là một trường con của $\mathbb{C}$.
Bây giờ ta chứng minh $\lbrace 1,\sqrt{2} \rbrace$ là một cơ sở của không gian vector $\mathbb{Q}[\sqrt{2}]$ trên $\mathbb{Q}$.
Thật vậy, hiển nhiên $\lbrace 1,\sqrt{2} \rbrace$ là tập sinh của $\mathbb{Q}[\sqrt{2}]$. Giờ ta chứng minh tính tuyến tính độc lập của nó. Giả sử tồn tại $a,b \in \mathbb{Q}$ sao cho $a1 + b\sqrt{2} = 0$. Khi đó ta có $\sqrt{2} = -\frac{a}{b}$ nếu $b \neq 0$, mâu thuẫn với giả thiết $\sqrt{2}$ là số vô tỉ. Do đó $b=0$ và suy ra $a=0$. Vậy $\lbrace 1,\sqrt{2} \rbrace$ là một cơ sở của không gian vector $\mathbb{Q}[\sqrt{2}]$ trên $\mathbb{Q}$.
Suy ra $[\mathbb{Q}[\sqrt{2}]:\mathbb{Q}] = 2$.
b) Ta làm tương tự ý a) để kết luận $\mathbb{Q}[\sqrt{p}]$ là một trường con của $\mathbb{C}$ và $\lbrace 1,\sqrt{p} \rbrace$ là một cơ sở của không gian vector $\mathbb{Q}[\sqrt{p}]$ trên $\mathbb{Q}$. Do đó $[\mathbb{Q}[\sqrt{p}]:\mathbb{Q}] = 2$, chú ý ở đây ta cũng có $\mathbb{q}$ là số vô tỉ.
c) Tương tự
d) Với $\displaystyle x\neq 0$ ta xét hằng đẳng thức $\displaystyle A^{3} +B^{3} +C^{3} -3ABC=( A+B+C)\left( A^{2} +B^{2} +C^{2} -AB-BC-CA\right)$ và có nhận xét rằng $\displaystyle A^{3} +B^{3} +C^{3} =3ABC$ khi và chỉ khi $\displaystyle A+B+C=0$. Như vậy:
trong đó $\displaystyle A=a,\ B=b\sqrt[3]{2} ,\ C=c\sqrt[3]{4}$
Tiếp theo ta chứng minh $\lbrace 1, \sqrt[3]{2}, \sqrt[3]{4} \rbrace$ là một cơ sở của không gian vector $\mathbb{Q}[\sqrt[3]{2}]$ trên $\mathbb{Q}$.
Hiển nhiên nó là một hệ sinh của $\mathbb{Q}[\sqrt[3]{2}]$. Ta cần chứng minh rằng nó độc lập tuyến tính. Giả sử có $\displaystyle a,b,c\in \mathbb{Q}$ sao cho $\displaystyle a+b\sqrt[3]{2} +c\sqrt[3]{4} =0$. Bằng việc quy đồng mẫu số ta có thể giả sử $\displaystyle a,b,c\in \mathbb{Z}$. Như vậy ta có $\displaystyle a^{3} +2b^{3} +4c^{3} -6abc=0$. Suy ra $\displaystyle a\vdots 2$ và đặt $\displaystyle a=2a_{1}$ thay lại vào phương trình:
Một lần nữa ta lại có $\displaystyle b\vdots 2$ và đặt $\displaystyle b=2b_{1}$. Thay lại ta cũng có được $\displaystyle c\vdots 2$ và cứ như vậy $\displaystyle a_{1} \vdots 2$, v.v… nhưng do $\displaystyle a,b,c$ đều là số nguyên cho nên việc chia đôi như vậy sẽ phải dừng lại sau hữu hạn bước dẫn tới mâu thuẫn. Vậy ta có điều phải chứng minh.
Bài tập: Giả sử $u \in \mathbb{C}$. Cho biết khi nào thì $[\mathbb{Q}(u):\mathbb{Q}]=2$
Giải:
$[\mathbb{Q}(u):\mathbb{Q}]=2$ tương đương với việc $\mathbb{Q}(u)$ là một không gian vector trên $\mathbb{Q}$ có cơ sở gồm hai phần tử. Nhận thấy rằng $u \notin \mathbb{Q}$ vì nếu $u \in \mathbb{Q}$ thì $\mathbb{Q}(u) = \mathbb{Q}$ và bậc mở rộng sẽ là 1. Mặt khác, tập $\lbrace 1,u,u^2 \rbrace$ là phụ thuộc tuyến tính, tức là tồn tại $a,b,c\in \mathbb{Q}$ không đồng thời bằng 0 sao cho $u$ là một nghiệm của đa thức $f(x)=ax^2+bx+c$. Mặt khác do $u \notin \mathbb{Q}$ cho nên $a \neq 0$. Hơn nữa $f(x)$ cũng phải là đa thức bất khả quy trên $\mathbb{Q}$ vì nếu không thì $u$ sẽ là nghiệm hữu tỉ.
Do đó $\Delta = b^2-4ac$ không là bình phương của một số hữu tỉ cho nên $u$ có dạng $u=r \pm \sqrt{s}$ với $r,s \in \mathbb{Q}, s \neq k^2, k \in \mathbb{Q}$.
Chiều ngược lại thì làm tương tự như bài trước đó.
Mở rộng đơn
Định nghĩa. CHo $F$ là một mở rộng của $K$. Khi đó, ta nói rằng $F$ là một mở rộng đơn của $K$ nếu tồn tại một phần tử $u \in F$ sao cho $F=K(u)$. $u$ lúc này được gọi là phần tử nguyên thủy của $F$.
Giả sử $F$ là một mở rộng của trường $K$ và $u \in F$. Phần tử $u$ được gọi là đại số trên $K$ nếu tồn tại một đa thức bậc dương $f(x) \in K[x]$ sao cho $f(u)=0$. Ngược lại, trong trường hợp $u$ không là nghiệm của bất kì một đa thức bậc dương nào trên $K$ thì $u$ được gọi là phần tử siêu việt trên $K$.
Ví dụ: $\sqrt{2}$ là đại số trên $\mathbb{Q}$ vì nó là nghiệm của đa thức $x^2-2$. Ngược lại, số $\pi$ là phần tử siêu việt trên $\mathbb{Q}$.
Cho $F$ là một mở rộng của trường $K$ và $u \in F$ là phần tử đại số trên $K$. Khi đó tồn tại một đa thức $p(x) \in K[x]$ bất khả quy nhận $u$ làm nghiệm. Hơn nữa, nếu $u$ là nghiệm của một đa thức $f(x) \in K[x]$ thì $f(x)$ chia hết cho $p(x)$. Đa thức $p(x)$ được gọi là đa thức tối thiểu của $u$ trên $K$.
Một số ứng dụng của lí thuyết Galois
Nghiệm phức
Ta gọi một biểu thức $f$ có dạng
trong đó $X$ là biến số còn $c_{i}$ là những hệ số cho trước là một đa thức. Số $n$ được gọi là bậc của đa thức $f$ và được kí hiệu là $\deg (f)$. Hệ số đầu là $c_{0}$ và hệ số tự do là $c_{n}$.
Phương trình đại số là một phương trình có dạng $f(X)=0$, trong đó $f$ là một đa thức bậc dương. Khi đó $\deg (f)$ được gọi là bậc của phương trình.
Như ta đã học ở cấp 2 thì không phải phương trình nào cũng có nghiệm thực. Chẳng hạn xét phương trình bậc 2 như sau
có nghiệm khi và chỉ khi biệt thức $\Delta =b^{2} -4ac$ không âm. Trường hợp giá trị này âm thì phương trình có nghiệm phức.
Định lí sau đây được gọi là định lí cơ bản của đại số. Nó cho thấy nếu ta mở rộng việc xét nghiệm lên các số phức thì mọi phương trình đại số với hệ số thực đều có nghiệm phức.
Định lí 1. Mọi phương trình đại số với hệ số phức đều có nghiệm trong tập số phức.
Chứng minh định lí này nằm ngoại phạm vi của bài viết nên mình xin phép không đề cập tới. Mọi người có thể tự tham khảo thêm các nguồn trên mạng nếu có hứng thú.
Việc xét nghiệm của một phương trình đại số có thể quy về bài toán phân tích đa thức thành các thừa số có dạng $X-a$.
Bổ đề 2. Đa thức $f(X)$ có nghiệm là $a$ khi và chỉ khi $f(X)$ có thể viết dưới dạng $f(X)=(X-a)g(X)$ với $g(X)$ là một đa thức.
Như vậy ta lại có được kết quả như dưới đây:
Định lí 3. Mọi đa thức $f(X)\neq 0$ với hệ số phức đều có thể viết dưới dạng
trong đó $c$ là một số phức, $a_{1} ,…,a_{r}$ là các số phức khác nhau và $n_{1} ,…,n_{r}$ là các số nguyên dương.
Ta có thể chứng minh kết quả trên bằng quy nạp và bổ đề 2.
Hệ quả 4. Mọi phương trình đại số bậc $n\geqslant 0$ với hệ số phức đều có đúng $n$ nghiệm phức, kể cả bội số.
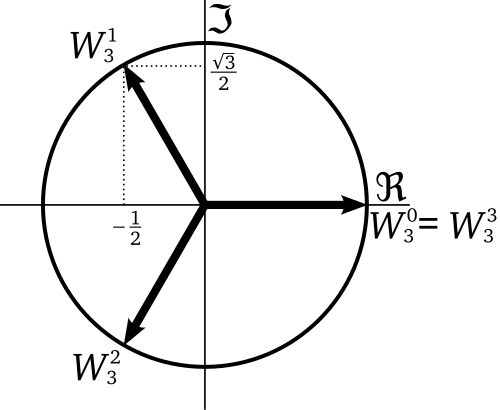
Ví dụ. Xét phương trình dạng $X^{n} -1=0$.Đặt
Từ công thức De Moivre ta có:
Cho nên $1,\epsilon,…,\epsilon^{n-1}$ là $n $ số phức khác nhau và chúng cùng chia vòng tròn đơn vị thành $n$ phần bằng nhau.
Hệ số của một đa thức có mối liên hệ chặt chẽ với nghiệm của đa thức thông qua các công thức sau đây, được gọi là hệ thức Viet.
Bổ đề 5. Cho $f=X^n+c_1X^{n-1}+…+c_n$. Các số $a_1,a_2,…,a_n$ (không nhất thiết phải khác nhau) là các nghiệm của $f$ khi và chỉ khi với mọi $t=1,2,…,n$ ta có: