Lattice Methods

Đại số tuyến tính

Giới thiệu lại một số khái niệm cơ bản

Không gian Vector

Khái niệm không gian vector là một trong những trụ cột quan trọng của bộ môn đại số tuyến tính. Việc hiểu rõ bản chất của không gian vector giúp ta xây dựng một nền tảng vững chắc phục vụ cho việc tiếp cận các khái niệm cao cấp hơn sau này. Trong bài viết này tác giả sẽ trình bày vắn tắt lại một số kết quả quan trọng liên quan đến không gian vector.

Khái niệm

Ta sẽ quy ước $\text{K}$ là một trường.

Định nghĩa 1. Không gian vector

Tập hợp $V$ được gọi là một không gian vector trên $\text{K}$ nếu nó được trang bị hai phép toán, phép toán đầu tiên là phép cộng hai vector, kí hiệu là $+$, phép toán thứ hai là phép nhân một vector với vô hướng $a$, kí hiệu là $\times$. Cụ thể, như sau

• Phép cộng hai vector : là một ánh xạ $+:V\times V\to V$ , ví dụ $(\alpha ,\beta )\to \alpha +\beta$
• Phép nhân hai vector: là một ánh xạ $\times :\text{K}\times V\to V$ , ví dụ : $(a,\alpha )\to a\alpha$ với $a\in \text{K},\alpha \in V$

Ngoài ra $V$ cũng thỏa mãn tính chất là một nhóm Abel đối với phép cộng và các mệnh đề về phân phối, giao hoán tương tự như khi làm việc trên tập số thực. Ở đây ta gọi các phần tử của $V$ là các vector còn các phần tử của $\text{K}$ là các vô hướng.

Độc lập tuyến tính và phụ thuộc tuyến tính

Định nghĩa 2. Tổ hợp tuyến tính, biểu thị tuyến tính

• Một tổ hợp tuyến tính của các vector ${\alpha }_1,{\alpha }_2,...,{\alpha }_n\in V$ là một biểu thức có dạng

$$\begin{array}{c}\sum _{i=1}^n{a}_i{\alpha }_i=a_1{\alpha }_1+...+a_n{\alpha }_n\end{array}$$

trong đó $a_i\in \text{K}$ là các vô hướng.

• Giả sử $\alpha =a_1{\alpha }_1+...+a_n{\alpha }_n$ thì ta nói rằng vector $\alpha$ biểu thị tuyến tính được qua hệ các vector ${\alpha }_1,...,{\alpha }_n$.

Ngoài ra một vector có thể có nhiều biểu thị tuyến tính khác nhau qua các hệ vector phân biệt. Biểu thị tuyến tính cũng có tính chất bắc cầu, tức là với hệ vector $({\alpha }_1,...,{\alpha }_n)$, ta nói hệ biểu diễn được qua hệ vector $({\beta }_1,...,{\beta }_m)$ nếu như mỗi vector trong hệ $({\alpha }_1,...,{\alpha }_n)$ đều biểu thị tuyến tính được qua hệ $({\beta }_1,...,{\beta }_m)$, và tương tự nếu hệ $({\beta }_1,...,{\beta }_m)$ biểu thị tuyến tính được qua hệ $({\gamma }_1,...,{\gamma }_k)$ thì khi đó hệ $({\alpha }_1,...,{\alpha }_n)$ biểu thị tuyến tính được qua hệ $({\gamma }_1,...,{\gamma }_k)$.

Định nghĩa 3. Độc lập tuyến tính và phụ thuộc tuyến tính.

Hệ $({\alpha }_1,...,{\alpha }_n)$ được gọi là độc lập tuyến tính nếu hệ thức

$$\begin{array}{c}{a}_1{\alpha }_1+...+a_n{\alpha }_n=0\end{array}$$

xảy ra khi và chỉ khi $a_1=...=a_n=0$

Ngược lại hệ $({\alpha }_1,...,{\alpha }_n)$ được gọi là phụ thuộc tuyến tính nếu hệ thức trên xảy ra và có ít nhất một giá trị $a_i\ne 0$

Cơ sở và số chiều của không gian vector

Định nghĩa 4. Hệ sinh và cơ sở

a/ Một hệ vector của $V$ được gọi là một hệ sinh của $V$ nếu mọi vector của $V$ đều biểu thị tuyến tính được qua hệ đó.
b/ Một hệ vector của $V$ được gọi là một cơ sở của $V$ nếu mọi vector của $V$ đều được biểu thị tuyến tính một cách duy nhất qua hệ đó.

Từ đây ta có các khẳng định sau về hệ sinh và cơ sở là tương đương nhau

i/ $({\alpha }_1,...,{\alpha }_n)$ là một cơ sở của $V$
ii/ $({\alpha }_1,...,{\alpha }_n)$ là một hệ sinh độc lập tuyến tính của $V$
iii/ $({\alpha }_1,...,{\alpha }_n)$ là một hệ vector độc lập tuyến tính cực đại của $V$.

Chứng minh đơn giản như sau:

Từ i/ suy ra ii/ : $({\alpha }_1,...,{\alpha }_n)$ là một cơ sở của $V$. Với ràng buộc tuyến tính $0=0{\alpha }_1+...+0{\alpha }_n$ thì vì $({\alpha }_1,...,{\alpha }_n)$ là một cơ sở của $V$ nên biểu diễn trên là duy nhất kéo theo $({\alpha }_1,...,{\alpha }_n)$ là một hệ sinh độc lập tuyến tính của $V$

Từ ii/ suy ra iii/ : $({\alpha }_1,...,{\alpha }_n)$ là một hệ sinh độc lập tuyến tính đồng nghĩa với việc mọi vector trong $V$ đều được biểu thị tuyến tính qua hệ và nó cũng là một hệ vector độc lập tuyến tính cực đại vì với $\beta \in V$ bất kì thì $\beta$ biểu thị tuyến tính được qua $({\alpha }_1,...,{\alpha }_n)$ cho nên $({\alpha }_1,...,{\alpha }_n,\beta )$ không còn độc lập tuyến tính

Từ iii/ qua i/ : Một hệ vector độc lập tuyến tính cực đại trong $V$ thì với mọi vector $\beta$ khác thuộc $V$ đều phải được biểu thị tuyến tính qua hệ này, có nghĩa là hệ này sinh ra $V$ và biểu diễn này là duy nhất. Vì giả sử rằng có hai biểu diễn là khác nhau tức là có ít nhất hai hệ số khác nhau giữa hai biểu diễn. Nếu lấy hiệu thì hệ không còn độc lập tuyến tính sinh ra mâu thuẫn.

Định nghĩa 5. Hữu hạn sinh

• Một không gian vector được gọi là hữu hạn sinh nếu như nó có một hệ sinh gồm hữu hạn phần tử.

Định nghĩa 6. Chiều của không gian

• Số phần tử của mỗi cơ sở của $K$-không gian vector hữu hạn sinh $V\ne \{0\}$ được gọi là số chiều của $V$ trên trường $K$. Kí hiệu là $\dim V$. Quy ước $\dim V=0$ khi $V=\{0\}$.

Định lí. Giả sử $V\ne \{0\}$ là một không gian vector hữu hạn sinh. Khi đó, $V$ có một cơ sở gồm hữu hạn phần tử. Hơn nữa, mọi cơ sở của $V$ đều có số phần tử bằng nhau.

Chứng minh.

Trước hết ta có một bổ đề sau: Trong không gian vector $V$, giả sử hệ vector $({\alpha }_1,...,{\alpha }_r)$ độc lập tuyến tính và biểu thị tuyến tính được qua hệ $({\beta }_1,...,{\beta }_s)$ thì ta có $r⩽s$.

Ta chứng minh bổ đề trên như sau: Theo giả thiết ta có một biểu thị tuyến tính như sau

$$\begin{array}{c}{\alpha }_1=a_1{\beta }_1+...+{\beta }_s\end{array}$$

Vì hệ $({\alpha }_1,...,{\alpha }_n)$ độc lập tuyến tính cho nên ta có thể giả sử ${\alpha }_1\ne 0$ và giả sử không mất tính tổng quát rằng $a_1\ne 0$. Khi đó ${\beta }_1$ có một biểu thị tuyến tính như sau:

$$\begin{array}{c}{\alpha }_1{a}_1^{-1}-\sum _{j=2}^s{\beta }_j\left(a_j{a}_1^{-1}\right)={\beta }_1\end{array}$$

Như vậy ${\beta }_1$ biểu thị tuyến tính được qua hệ $({\alpha }_1,{\beta }_2,...,{\beta }_s)$,và khi đó $({\alpha }_1,...,{\alpha }_r)$ biểu thị tuyến tính qua $({\beta }_1,...,{\beta }_s)$ còn $({\beta }_1,...,{\beta }_s)$ lại biểu thị tuyến tính được qua $({\alpha }_1,...,{\beta }_s)$ cho nên $({\alpha }_1,...,{\alpha }_r)$ biểu thị tuyến tính được qua $({\alpha }_1,...,{\beta }_s)$. Lí do có biểu diễn trên là vì: ta đã có ${\beta }_1$ biểu thị tuyến tính được qua $({\alpha }_1,...,{\beta }_s)$. Tương tự với ${\beta }_2$ cũng biểu thị tuyến tính được qua $({\alpha }_1,{\beta }_2,...,{\beta }_s)$ bằng cách lấy mọi vô hướng của các số ${\alpha }_1,{\beta }_i,i\ne 2$ đều bằng không thì ta có được một biểu thị tuyến tính.

Bây giờ tiếp tục ta sẽ chứng minh được rằng $({\alpha }_1,...,{\alpha }_r)$ biểu thị tuyến tính được qua $({\alpha }_1,..,{\alpha }_i,{\beta }_{i+1},...,{\beta }_s)$ trong đó $i⩽\min \{r,s\}$. Ta sẽ quy nạp. Đầu tiên với $i=1$ thì mệnh đề đúng theo điều vừa chỉ ra ở trên. Giả sử nó đúng tới $i$ và ta sẽ chứng minh $i+1$ cũng đúng trong trường hợp $i+1⩽\min \{r,s\}$.

Ta có $({\alpha }_1,...,{\alpha }_r)$ biểu thị tuyến tính được qua $({\alpha }_1,...,{\alpha }_i,{\beta }_{i+1},...,{\beta }_s)$. Như vậy ${\alpha }_{i+1}$ biểu thị tuyến tính được qua $({\alpha }_1,...,{\alpha }_i,{\beta }_{i+1},...,{\beta }_s)$ cho nên ta có

$$\begin{array}{c}{\alpha }_{i+1}=\sum _{j=1}^i{\gamma }_j^{(i+1)}{\alpha }_j+\sum _{j=i+1}^s{\lambda }_j^{(i+1)}{\beta }_j\end{array}$$

Ta có hệ $({\alpha }_1,...,{\alpha }_r)$ là một hệ độc lập tuyến tính cho nên khi đó có ít nhất một giá trị ${\lambda }_j^{i+1}\ne 0$ vì nếu không thì ${\alpha }_{i+1}$ biểu thị tuyến tính qua $({\alpha }_1,...,{\alpha }_i,...,{\alpha }_r)$ là mẫu thuẫn vì $({\alpha }_1,...,{\alpha }_r)$ là một hệ độc lập tuyến tính. Tương tự như trên ta cũng suy ra ${\beta }_{i+1}$ biểu thị tuyến tính được qua hệ $({\alpha }_1,...,{\alpha }_i,{\alpha }_{i+1},{\beta }_{i+2},...,{\beta }_s)$. Cho nên $({\alpha }_1,..,{\alpha }_i,{\beta }_{i+1},...,{\beta }_s)$ biểu thị tuyến tính qua hệ $({\alpha }_1,...,{\alpha }_i,{\alpha }_{i+1},{\beta }_{i+2},...,{\beta }_s)$. Suy ra ta có điều phải chứng minh. Bây giờ nếu $r>s$ thì ta suy ra $i=s$. Khi đó $({\alpha }_1,...,{\alpha }_r)$ biểu thị tuyến tính qua hệ $({\alpha }_1,...,{\alpha }_s)$ là mâu thuẫn với giả sử hệ độc lập tuyến tính. Vậy $r⩾s$.

Bây giờ ta sẽ quay trở lại chứng minh định lí ban đầu.

Giả sử $({\gamma }_1,...,{\gamma }_s)$ là một hệ sinh hữu hạn của $V$. Ta gọi $({\alpha }_1,...,{\alpha }_r)$ là một hệ độc lập tuyến tính trong $V$. Hệ này biểu thị tuyến tính được qua $({\gamma }_1,...,{\gamma }_s)$ theo định nghĩa của hệ sinh. Suy ra theo bổ đề thì $r⩽s$. Ta tiếp tục bổ sung vào trong hệ $({\alpha }_1,...,{\alpha }_r)$ các vector để sao cho hệ vẫn là hệ độc lập tuyến tính và rõ ràng, quá trình này phải dừng lại sau hữu hạn bước và hệ thu được là hệ vector độc lập tuyến tính cực đại trong $V$. Vì là hệ vector độc lập tuyến tính cực đại nên mỗi vector trong $V$ được biểu thị duy nhất qua hệ này. Suy ra ta có điều phải chứng minh.

Cuối cùng là một định lí, có thể coi như là hệ quả của kết quả trên.

Định lí. Giả sử $V$ là một không gian vector hữu hạn sinh. Khi đó mọi hệ sinh của $V$ đều chứa một cơ sở. Mọi hệ độc lập tuyến tính trong $V$ đều có thể được bổ sung để trở thành một cơ sở của $V$. Nếu $\dim V=n$, thì mọi hệ độc lập tuyến tính gồm $n$ vector của $V$ đều là một cơ sở.

Ngoài ra người ta cũng nhận xét được rằng, trong một không gian vector vô hạn sinh (tức là không hữu hạn sinh), hai cơ sở bất kì đều có cùng lực lượng. Nhưng một hệ vector độc lập tuyến tính có cùng lực lượng với cơ sở thì không nhất thiết là một cơ sở.

Định nghĩa 7. Tọa độ

Bộ vô hướng $(a_1,...,a_n)$ xác định bởi điều kiện $\alpha =\sum _{i=1}^n{a}_i{\alpha }_i$ được gọi là tọa độ của vector $\alpha$ trong cơ sở $({\alpha }_1,{\alpha }_2,...,{\alpha }_n)$. Vô hướng $a_i$ được gọi là tọa độ thứ $i$ của $\alpha$ trong cơ sở đó.

Bây giờ ta cùng xem xét tọa độ của một vector trong những cơ sở khác nhau thì có liên quan với nhau như thế nào. Xét hai cơ sở $({\beta }_1,...,{\beta }_n)$ và $({\alpha }_1,...,{\alpha }_n)$ của không gian vector $V$. Như vậy mỗi vector ${\beta }_i$ biểu thị tuyến tính được qua $({\alpha }_1,...,{\alpha }_n)$ tức là có các số ${\gamma }_i^{(j)}$ sao cho

$$\begin{array}{c}{\beta }_j=\sum _{i=1}^n{\gamma }_i^{(j)}{\alpha }_i\end{array}$$

Giả sử $\alpha$ có tọa độ lần lượt là $(a_1,...,a_n)$ và $(b_1,...,b_n)$ trong hai cơ sở $({\alpha }_1,...,{\alpha }_n)$ và $({\beta }_1,...,{\beta }_n)$. Thì khi đó

$$\begin{array}{c}\alpha =\sum _{j=1}^n{b}_j{\beta }_j=\sum _{j=1}^n{b}_j\sum _{i=1}^n{\gamma }_i^{(j)}{\alpha }_i=\sum _{j=1}^n\left(\sum _{i=1}^n{b}_j{\gamma }_i^{(j)}\right){\alpha }_i=\sum _{j=1}^n{a}_j{\alpha }_j\end{array}$$

Và do mỗi biểu thị tuyến tính của $\alpha$ trong $({\alpha }_1,...,{\alpha }_n)$ là duy nhất cho nên ta có

$$\begin{array}{c}{a}_j=\sum _{i=1}^n{b}_j{\gamma }_i^{(j)},j=1,2,...,n\end{array}$$

Không gian con - Hạng của một hệ vector

Định nghĩa 8. Không gian con

Tập con không rỗng $W\subset V$ được gọi là một không gian vector con của $V$ nếu như $W$ cũng đóng kín đối với hai phép toán trên $V$, tức là

$$\begin{array}{c}\alpha +\beta \in W,\forall \alpha ,\beta \in W\\ a\alpha \in W,\forall a\in \text{K},\alpha \in W\end{array}$$

Mệnh đề 1. Nếu $W$ là một không gian vector con của $V$ thì ta cũng có $\dim W⩽\dim V$.

Kết quả trên là hệ quả trực tiếp của khái niệm về số chiều của một không gian vector. Cụ thể với mỗi hệ độc lập tuyến tính trong $W$ thì cũng độc lập tuyến tính trong $V$. Ngoài ra mỗi phần tử của hệ độc lập tuyến tính đều được biểu thị tuyến tính thông qua cơ sở của $V$ cho nên ta có $\dim W⩽\dim V$. Dấu bằng xảy ra khi và chỉ khi $\dim W=\dim V=n$ hay $W=V$, tức là khi đó mọi cơ sở của $W$ cũng là cơ sở của $V$

Mệnh đề 2. Giao của một họ bất kì các không gian vector con của $V$ cũng là một không gian vector con của $V$.

Thật vậy, xét một họ các không gian vector con của $V$ là $\{V_i{\}}_{i\in I}$ thì khi đó ${\cap }_{i\in I}{V}_i$ cũng thỏa mãn tính đóng đối với phép cộng và nhân.

Định nghĩa 9. Không gian vector sinh bởi $X$

Giả sử $X$ là một tập con của không gian vector $V$. Giao của tất cả các không gian vector con của $V$ mà chứa $X$ được gọi là không gian vector con của $V$ sinh bởi $X$ và được kí hiệu là $\mathcal{L}(X)$.

Từ định nghĩa, ta suy ra được rằng $\mathcal{L}(X)$ là không gian vector con nhỏ nhất của $V$ mà chứa $X$

Khi đó $\mathcal{L}(X)$ là tập hợp các tổ hợp tuyến tính của các phần tử của $X$. Nói riêng nếu $X=\{{\gamma }_1,...,{\gamma }_k\}$ thì

$$\begin{array}{c}\mathcal{L}(X)=\left\{\sum _{i=1}^k{a}_i{\gamma }_i|a_i\in \text{K}\right\}\end{array}$$

Thật vậy, tập hợp các tổ hợp tuyến tính của $X$ chính là một không gian con của $V$ mà chứa $X$. Mặt khác, mọi tổ hợp tuyến tính của $X$ đều nằm trong mọi không gian vector con của $V$ mà chứa $X$. Vì với mỗi không gian vector con $W\subset V$ mà $W$ chứa $X$ thì khi đó các phần tử của $X$ cũng thỏa mãn tính đóng đối với phép cộng và nhân vô hướng trên $W$. Điều này dẫn tới mọi tổ hợp tuyến tính của $X$ cũng nằm trong $W$.

Tiếp theo ta xét về số chiều của $\mathcal{L}(X)$.

Nhận xét: Số chiều của không gian $\mathcal{L}(X)$ được gọi là hạng của tập hoặc hệ vector $X$ và được kí hiệu là $\text{rank}(X)$. Tương tự ta gọi một tập con các vector của $X$ là tuyến tính cực đại nếu như ta thêm bất kì vector nào trong $X$ vào tập đó thì tập sẽ trở thành tập con phụ thuộc tuyến tính. Như vậy, để tính hạng của $\mathcal{L}(X)$ ta sẽ đếm số vector của mỗi tập con độc lập tuyến tính cực đại trong $X$
.
Hệ quả: Hai tập con độc lập tuyến tính cực đại trong $\mathcal{L}(X)$ thì có số phần tử bằng nhau.

Tổng và tổng trực tiếp

Ta giả sử $W_1,...,W_n$ là các không gian vector con của $V$. Khi đó tập hợp

$$\begin{array}{c}{W}_1+...+W_n=\{{\alpha }_1+...+{\alpha }_n|{\alpha }_i\in W_i,i=1,..,n\}\end{array}$$

hiển nhiên lập nên một không gian vector con của $V$.

Định nghĩa 10. Tổng của các không gian vector

Không gian vector $\sum _{i=1}^n{W}_i$ được gọi là tổng của các không gian vector con $W_1,...,W_n$.

Khi đó mỗi vector $\alpha$ thuộc không gian vector trên có thể được viết dưới dạng

$$\alpha ={\alpha }_1+...+{\alpha }_n,{\alpha }_i\in W_i$$

Tuy vậy, cách viết trên không phải là duy nhất. Vì thế ta đi đến một khái niệm chặt hơn như sau.

Định nghĩa 11. Tổng trực tiếp

Nếu mọi vector trong không gian $\sum _{i=1}^n{W}_i$ đều được viết duy nhất dưới dạng $\alpha ={\alpha }_1+...+{\alpha }_n$ thì khi đó ta gọi $\sum _{i=1}^n{W}_i$ là tổng trực tiếp của các không gian vector $W_i$ và kí hiệu là $W_1\oplus ...\oplus W_n$. Từ định nghĩa trên ta đi đến các tính chất nhằm giúp ta xác định khi nào tổng trên thỏa mãn là một tổng trực tiếp của các không gian vector con.

Định lí. $\sum _{i=1}^n{W}_i$ là tổng trực tiếp khi và chỉ khi điều kiện sau đây được thỏa mãn:

$$W_i\cap \left(\sum _{j\ne i}{W}_j\right)=\{0\},i=1,2,...,n$$

Ta có định lí sau đây khi nói về số chiều của tổng các không gian vector:

Định lí. Giả sử $U$ và $W$ là một không gian vector con của một không gian vector $V$ hữu hạn chiều.
Khi đó ta có

$$\begin{array}{c}\dim U+\dim W=\dim (U+W)+\dim (U\cap W)\end{array}$$

Chứng minh.
Giả sử $\{{\alpha }_1,...,{\alpha }_r\}$ là một cơ sở cho $U\cap W$. Nếu $U\cap W=\{0\}$ thì ta coi như $r=0$. Ta bổ sung hệ này để có một cơ sở $\{{\alpha }_1,...,{\alpha }_r,{\beta }_1,...,{\beta }_s\}$ của $U$ và một cơ sở $\{{\alpha }_1,...,{\alpha }_r,{\gamma }_1,...,{\gamma }_t\}$ của $W$. Ta sẽ chứng minh rằng $\{{\alpha }_1,...,{\alpha }_r,{\beta }_1,...,{\beta }_s,{\gamma }_1,...,{\gamma }_t\}$ là một cơ sở của $U+W$. Rõ ràng $\{{\alpha }_1,...,{\alpha }_r,{\beta }_1,...,{\beta }_s,{\gamma }_1,...,{\gamma }_t\}$ là một hệ sinh của $U+W$.
Với mỗi $\alpha \in U+W$ được viết dưới dạng

$$\begin{array}{c}\alpha =\text{u}+\text{w},\text{u}\in U,\text{w}\in W\end{array}$$

Bây giờ, để chứng minh tính độc lập tuyến tính, ta giả sử có một ràng buộc tuyến tính

$$\begin{array}{c}{a}_1{\alpha }_1+...+a_r{\alpha }_r+b_1{\beta }_1+...+b_s{\beta }_s+c_1{\gamma }_1+...c_t{\gamma }_t=0\end{array}$$

với $a_i,b_j,c_k\in \text{K}$. Ta cần chứng minh $a_i=b_i=c_i=0,\forall i$. Xét đẳng thức sau đây:

$$\begin{array}{c}{a}_1{\alpha }_1+...+a_r{\alpha }_r+b_1{\beta }_1+...+b_s{\beta }_s=-(c_1{\gamma }_1+...c_t{\gamma }_t)\end{array}$$

Vector bên trái thuộc vào $U$ và vector bên phải thuộc vào $W$ vì nó là vector sinh bởi cơ sở của $W$. Như vậy vector trên thuộc vào $U\cap W$. Do đó nó cũng có một biểu diễn tuyến tính qua $({\alpha }_1,...,{\alpha }_r)$ như sau

$$\begin{array}{c}{d}_1{\alpha }_1+...+d_r{\alpha }_r=-(c_1{\gamma }_1+...c_t{\gamma }_t)\\ \leftrightarrow c_1{\gamma }_1+...c_t{\gamma }_t+d_1{\alpha }_1+...+d_r{\alpha }_r=0\end{array}$$

Nhưng do hệ $({\alpha }_1,...{\alpha }_r,{\gamma }_1,...,{\gamma }_t)$ độc lập tuyến tính cho nên $d_1=...=d_r=c_1=...=c_t=0$. Như vậy thay ngược lại ở trên ta có

$$\begin{array}{c}{a}_1{\alpha }_1+...+a_r{\alpha }_r+b_1{\beta }_1+...+b_s{\beta }_s=0\end{array}$$

Và một lần nữa do $({\alpha }_1,...,{\alpha }_r,{\beta }_1,...,{\beta }_s)$ là một hệ độc lập tuyến tính cho nên $a_1=...=a_r=b_1=...=b_s=0$. Vậy ta có điều phải chứng minh. Từ những nhận xét trên ta suy ra $\{{\alpha }_1,...,{\alpha }_r,{\beta }_1,...,{\beta }_s,{\gamma }_1,...,{\gamma }_t\}$ là cơ sở của $U+W$.

Từ định nghĩa về tổng trực tiếp ta cũng suy ra ngay

$$\begin{array}{c}\dim (U\oplus W)=\dim (U)+\dim (W)\end{array}$$

Định nghĩa 12. Phần bù tuyến tính

Nếu $V=U\oplus W$ thì $W$ được gọi là một phần bù tuyến tính của $U$ trong $V$ và $\dim W=\dim V-\dim U$ được gọi là đối chiều của $U$ trong $V$. Giả sử $V=U\oplus W$. Khi đó mỗi vector trong $v$ có thể được biểu diễn duy nhất dưới $v=u+w$.

Định nghĩa một ánh xạ

$$\begin{array}{c}p{r}_U:V\to U\\ p{r}_U(v)=u\end{array}$$

Nó được gọi là phép chiếu từ $V$ lên $U$ theo phương $W$. Phép chiếu có các tính chất sau:

$$\begin{array}{c}p{r}_U(v+v^{\prime })=p{r}_U(v)+p{r}_U(v^{\prime }),\forall v,v^{\prime }\in V\\ p{r}_U(av)=ap{r}_U(v),\forall v\in V\end{array}$$

Không gian thương - Quotient Spaces

Đầu tiên ta có định nghĩa về quan hệ tương đương.

Định nghĩa. Một quan hệ tương đương trên một tập hợp $A$ là một mối quan liên hệ $x\sim y$ giữa các phần tử $x,y$ của $A$ thỏa mãn đồng thời các điều kiện sau:

• Tính phản xạ : $x\sim x$ với mọi $x\in A$
• Tính đối xứng: Nếu $x\sim y$ thì $y\sim x$
• Tính bắc cầu: Nếu $x\sim y$ và $y\sim z$ thì $x\sim z$

Lattice

Qui ước

Các kí hiệu: Các vector với các phần tử trong $\mathbb{R}$ được xem như là vector cột và được biểu thị bằng các chữ in thường đậm, ví dụ $\mathbf{x},\mathbf{y},\mathbf{z}$. Các ma trận được biểu thị bằng các chữ cái in hoa đậm, ví dụ $\mathbf{A},\mathbf{S},\mathbf{B},...$
Chuyển vị của một vector hoặc ma trận được biểu thị bằng ${\mathbf{v}}^T$ hoặc ${\mathbf{V}}^T$ tương ứng. Ngoài ra, chúng ta biểu thị tích trong của hai vector cột $\mathbf{v},\mathbf{w}\in {\mathbb{R}}^n$ theo $⟨\mathbf{v},\mathbf{w}⟩={\mathbf{v}}^T\mathbf{w}$.
Một số kí hiệu khác:

• ${\mathbb{R}}^{n\times m}$: không gian của ma trận $n\times m$ với các mục số thực
• $\Vert \cdot \Vert ,\Vert \cdot {\Vert }_{\infty }$: Chuẩn Euclid và chuẩn tối đa
• $\mathcal{L}$: Một lưới
• $\mathcal{L}(\mathbf{B})$: lưới với các cột của ma trận $\mathbf{B}$ làm cơ sở.
• ${\lambda }_i(\mathcal{L})$: Số nhỏ nhất sao cho có $i$ vector độc lập tuyến tính trong $\mathcal{L}$ mà mỗi vector đó có chuẩn không vượt quá ${\lambda }_i$.
• $\gamma$ : Hệ số xấp xỉ (gần đúng) trong các bài toán lưới
• ${\mathbf{b}}_i$: một vector cơ sở lưới
• ${\mathbf{b}}_i^{\ast }$: một vector trong cơ sở trực giao Gram-Schmidt của một lưới.

Mở đầu

Nhắc lại một số định nghĩa

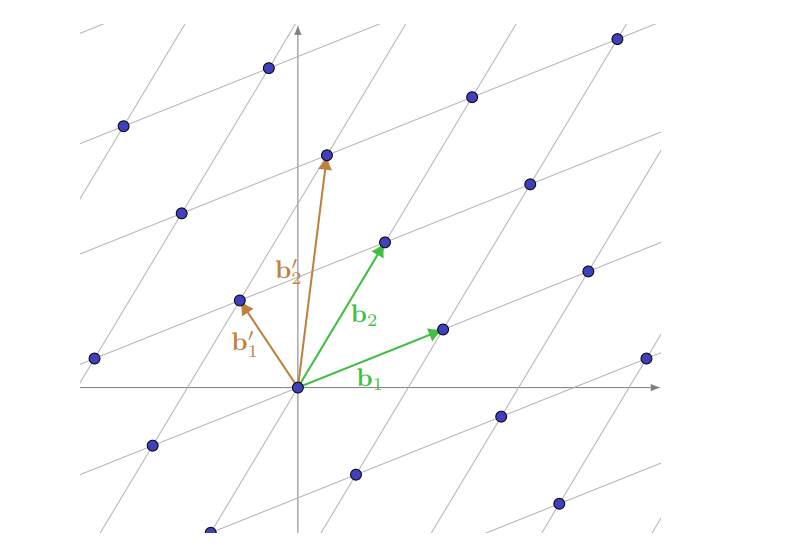
Một lattice $\mathcal{L}\subset {\mathbb{R}}^m$ là một không gian vector được sinh bởi các tổ hợp tuyến tính nguyên của các vector độc lập tuyến tính. Tức là

$$\begin{array}{c}\mathcal{L}=\left\{\sum _{i=1}^n{x}_i{\mathbf{b}}_i|x_i\in \mathbb{Z}\right\}\end{array}$$

trong đó $\{{\mathbf{b}}_i{\}}_{i=1}^n\subset {\mathbb{R}}^m$. Đặt $\mathbf{B}\in {\mathbb{R}}^{m\times n}$ thì $\mathcal{L}=\mathbf{B}{\mathbb{Z}}^n$, đồng nghĩa với việc $\mathcal{L}$ là ảnh của ${\mathbb{Z}}^n$ dưới ánh xạ tuyến tính $\mathbf{B}:{\mathbb{R}}^n\to {\mathbb{R}}^m$.

Ta có thể định nghĩa lưới theo một cách khác. Cho $m,n,k\in {\mathbb{Z}}_{>0}$ với $m⩾k$. Một lưới $m$ chiều $\mathcal{L}$ là một nhóm con cộng rời rạc của ${\mathbb{R}}^m$ chứa tất cả các tổ hợp tuyến tính nguyên của $k$ vector độc lập tuyến tính $\{{\mathbf{b}}_1,{\mathbf{b}}_2,...,{\mathbf{b}}_k\}$. Đó là $\mathcal{L}=\left\{\mathbf{Bx}|\mathbf{x}\in {\mathbb{Z}}^k\right\}$ với ma trận $\mathbf{B}=({\mathbf{b}}_1,...,{\mathbf{b}}_k)\in {\mathbb{R}}^{m\times k}$. Ta gọi $\mathbf{B}$ là cơ sở của $\mathcal{L}$ và $k$ là rank của lưới. Sau này ta chỉ quan tâm tới các full rank lattice tức là các lattice có hạng bằng với số chiều.

Định thức của một lưới $\mathcal{L}$ với cơ sở $\mathbf{B}$ được xác định bởi $\det (\mathcal{L})=\sqrt{|\det \left({\mathbf{B}}^T\mathbf{B}\right)|}$. Nếu lattice $\mathcal{L}$ là full rank thì $\det (\mathcal{L})=|\det (\mathbf{B})|$.

Lưu ý rằng cơ sở của một lưới không là duy nhất, hay nói đúng hơn với mỗi ma trận đơn nhất $\mathbf{U}\in {\mathbb{Z}}^{n\times n}$ thì $\mathbf{BU}$ cũng là cơ sở cho cùng một lưới. Vì ta có tính chất sau: Với hai cơ sở $\mathbf{B}$ và ${\mathbf{B}}^{\prime }$ cho lưới $\mathcal{L}$ thì $\mathcal{L}(\mathbf{B})=\mathcal{L}({\mathbf{B}}^{\prime })$ cho nên suy ra $\det (\mathbf{B})=\det ({\mathbf{B}}^{\prime })$.

Một ma trận đơn nhất $\mathbf{U}$ là một ma trận thỏa mãn $\det (\mathbf{U})=1$. Như vậy nếu ta lấy ${\mathbf{B}}^{\prime }=\mathbf{BU}$ thì sẽ thỏa mãn định thức hai ma trận trên là như nhau.

Tính chất trên tuy đơn giản nhưng rất quan trọng đối với việc triển khai các hệ mật, vì một số cơ sở dễ xử lí hơn những cơ sở khác.

Mỗi lưới $\mathcal{L}$ có một lưới đối ngẫu (dual lattice), kí hiệu ${\mathcal{L}}^{\ast }=\left\{\mathbf{w}\in {\mathbb{R}}^m|⟨\mathbf{w},\mathbf{x}⟩\in \mathbb{Z},\forall \mathbf{x}\in \mathcal{L}\right\}$.

Các bài toán khó

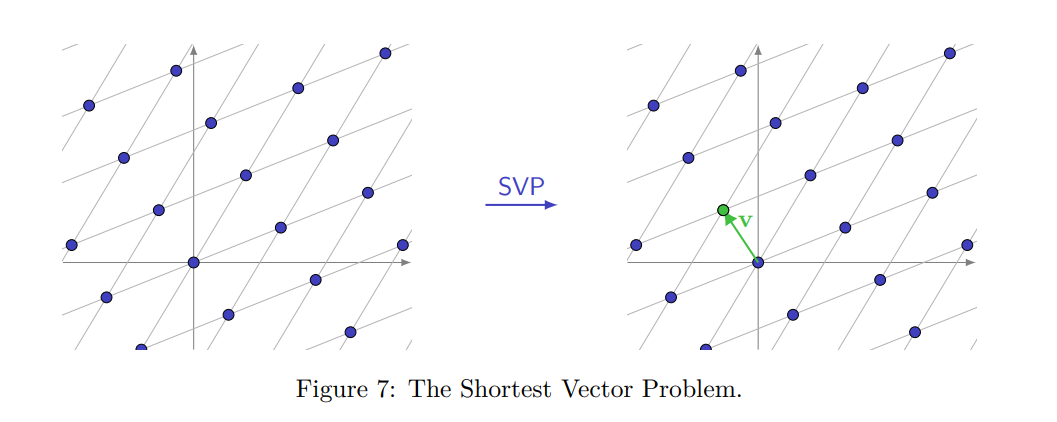
Bài toán tìm vector ngắn nhất - SVP : Cho một cơ sở tùy ý $\mathbf{B}$ của một lưới $\mathcal{L}$ có số chiều $m$, hãy tìm một $x\in \mathcal{L}$ khác không với $\Vert x\Vert ⩽\gamma (m){\lambda }_1(\mathcal{L})$

Trong đó ${\lambda }_1(\mathcal{L})$ là độ dài cực tiểu thứ nhất của lưới $\mathcal{L}$ (first successive minimum). Mà theo định lí thứ nhất của Minkowski thì với một full rank lattice $\mathcal{L}$ với rank là $n$ thì

$$\begin{array}{c}{\lambda }_1(\mathcal{L})⩽\sqrt{n}\mid \det (\mathcal{L}){\mid }^{1/n}\end{array}$$

Hiểu một cách trực quan: ${\lambda }_i(\mathcal{L})$ là bán kính của một quả cầu có tâm tại gốc tọa độ sao cho trong quả cầu đó tồn tại $i$ vector độc lập tuyến tính.

Biến thể của bài SVP là bài uSVP là tìm vector ngắn nhất và duy nhất.

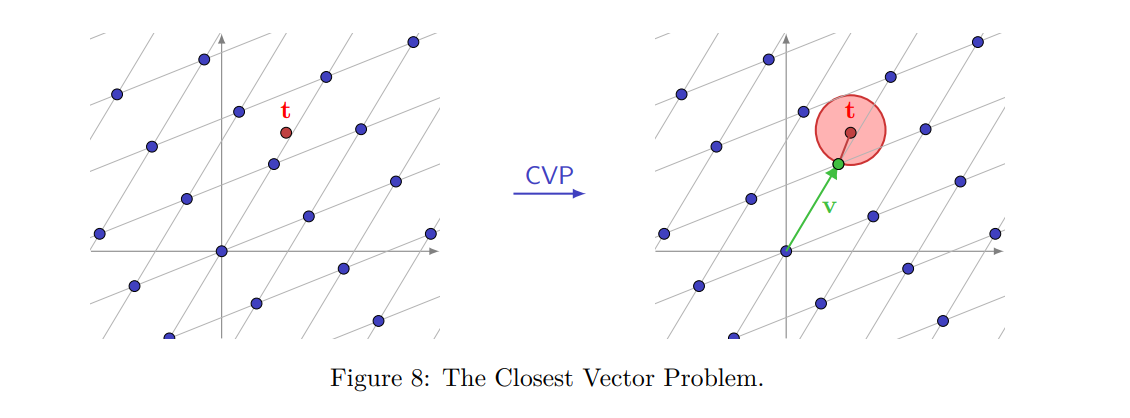
Bài toán vector gần nhất - CVP: Cho một cơ sở tùy ý $\mathbf{B}$ của một lưới $\mathcal{L}=\mathcal{L}(\mathbf{B})$ và một vector đích $\mathbf{t}$ (không nhất thiết thuộc vào $\mathcal{L}$). Tìm một vector $\mathbf{v}$ thuộc lưới sao cho $\Vert \mathbf{v}-\mathbf{t}\Vert =\underset{\mathbf{w}\in \mathcal{L}}{\min }\Vert \mathbf{w}-\mathbf{t}\Vert$.

Các thuật toán rút gọn lưới

Các thuật toán rút gọn lưới nhằm mục đích lấy một cơ sở đưa ra của một lưới và biến đổi nó thành một cơ sở khác cho cùng lưới nhưng với các vector ngắn hơn và trực giao hơn. Bằng cách này, một vector lưới ngắn có thể được khôi phục. Các thuật toán thường không được thiết kế để tìm chính xác, mà là để trích xuất một vector ngắn trong một số yếu tố gần đúng, nói cách khác là để giải một số bài toán lưới khó gần đúng.

Thuật toán Gram-Schmidt

Hai vector $\mathbf{u},\mathbf{v}$ được gọi là trực giao nếu như tích trong của chúng bằng 0 tức là $⟨\mathbf{u},\mathbf{v}⟩=0$. Một hệ các vector $\mathbf{S}=({\mathbf{v}}_1,...,{\mathbf{v}}_n)$ được gọi là một hệ trực giao nếu như chúng đôi một trực giao. Tương tự, một hệ trực giao các vector đơn vị được gọi là một hệ trực chuẩn.

Ta có thể chứng minh rằng mọi hệ trực chuẩn đều độc lập tuyến tính.

Định lí: Cho $\mathbf{S}=({\mathbf{v}}_1,...,{\mathbf{v}}_n)$ là một hệ các vector độc lập tuyến tính của không gian Euclid $V$. Khi đó ta có thể tìm được một hệ trực chuẩn ${\mathbf{S}}^{\prime }=({\mathbf{u}}_1,...,{\mathbf{u}}_n)$ sao cho

$$\begin{array}{c}span\{{\mathbf{v}}_1,..,{\mathbf{v}}_k\}=span\{{\mathbf{u}}_1,...,{\mathbf{u}}_k\},\forall k=1,...,n\end{array}$$

Để xây dựng một hệ trực chuẩn thì trước hết ta sẽ xây dựng một hệ trực giao rồi lấy từng vector chia cho chuẩn của chính nó.

from sage.all import *
 
def gram_schmidt(vectors):
    orthogonal_vectors = []
    for v in vectors:
        for u in orthogonal_vectors:
            v -= (v * u) / (u * u) * u
        orthogonal_vectors.append(v)
    return orthogonal_vectors
v1 = vector([4, 1, 3, -1])
v2 = vector([2, 1, -3, 4])
v3 = vector([1, 0, -2, 7])
v4 = vector([6, 2, 9, -5])
 
v = [v1,v2,v3,v4]
output = gram_schmidt(v)
print(output)

Thuật toán LLL

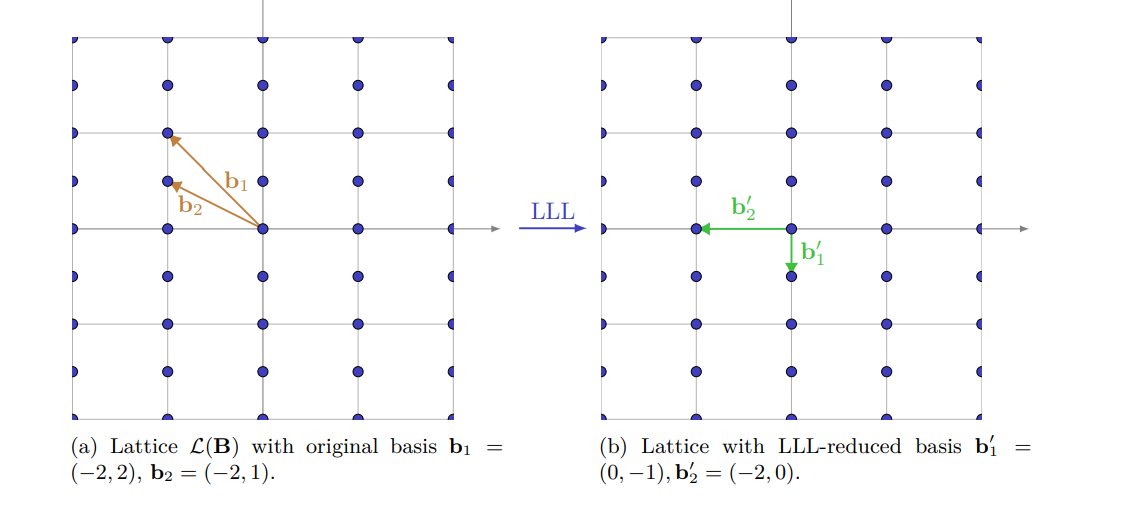
Thuật toán rút gọn lưới đầu tiên là LLL. Mục tiêu của thuật toán LLL là tìm ra một cơ sở ${\mathbf{b}}_i$ của lưới sao cho các vector Gram-Schmidt ${\mathbf{b}}_i^{\ast }$ không quá giảm về kích thước. Cụ thể, với $\delta \in (1/4,1)$ ta gọi một cơ sở $\mathbf{B}=\{{\mathbf{b}}_1,...,{\mathbf{b}}_n\}$ là một cơ sở rút gọn $\delta -LLL$ nếu như

1. $|{\mu }_{i,j}|⩽\frac{1}{2}$ với mọi $1⩽j<i$.
2. $\left(\delta -{\mu }_{i+1,i}^2\right)\Vert {\mathbf{b}}_i^{\ast }{\Vert }^2⩽\Vert {\mathbf{b}}_{i+1}^{\ast }{\Vert }^2,\forall 1⩽i⩽n-1$.

Phân tích: Thuật toán bắt đầu bằng việc tìm một cơ sở trực giao từ một cơ sở cho trước. Trong quá trình trực giao hóa Gram-Schmidt, sẽ có một số hệ số Gram-Schmidt thỏa mãn:

$${\mu }_{i,j}=\frac{\mid {\mathbf{v}}_i\cdot {\mathbf{v}}_j^{\ast }\mid }{\Vert \mathbf{v}{{}_j^{\ast }}^2\Vert }>\frac{1}{2}$$

Ta có thể giảm độ lớn của các hệ số này bằng cách lấy ${\mathbf{b}}_{\mathbf{i}}-a{\mathbf{b}}_{\mathbf{j}}$. Nếu có hai hàng không thỏa mãn điều kiện thứ hai thì ta sẽ swap 2 hàng này và lặp lại thuật toán. Bằng cách này ta sẽ làm giảm dần các hệ số ${\mu }_{i,j}$ và thu được một cơ sở rút gọn.

Mọi người có thể xem implement của key-moon tại đây https://github.com/key-moon/pylll/blob/main/pylll/lll.py

Cài đặt flatter Tham khảo tại link sau https://github.com/keeganryan/flatter.

Để cài thì đầu tiên cần clone repo về terminal của mình
git clone https://github.com/keeganryan/flatter.

Tool được build bằng cmake nên cần cài thêm như sau

sudo apt update
sudo apt install build-essential cmake

Tiếp theo tạo một thư mục build và chạy cmake

mkdir build
cd build
cmake ..

Mình gặp một cái lỗi như này

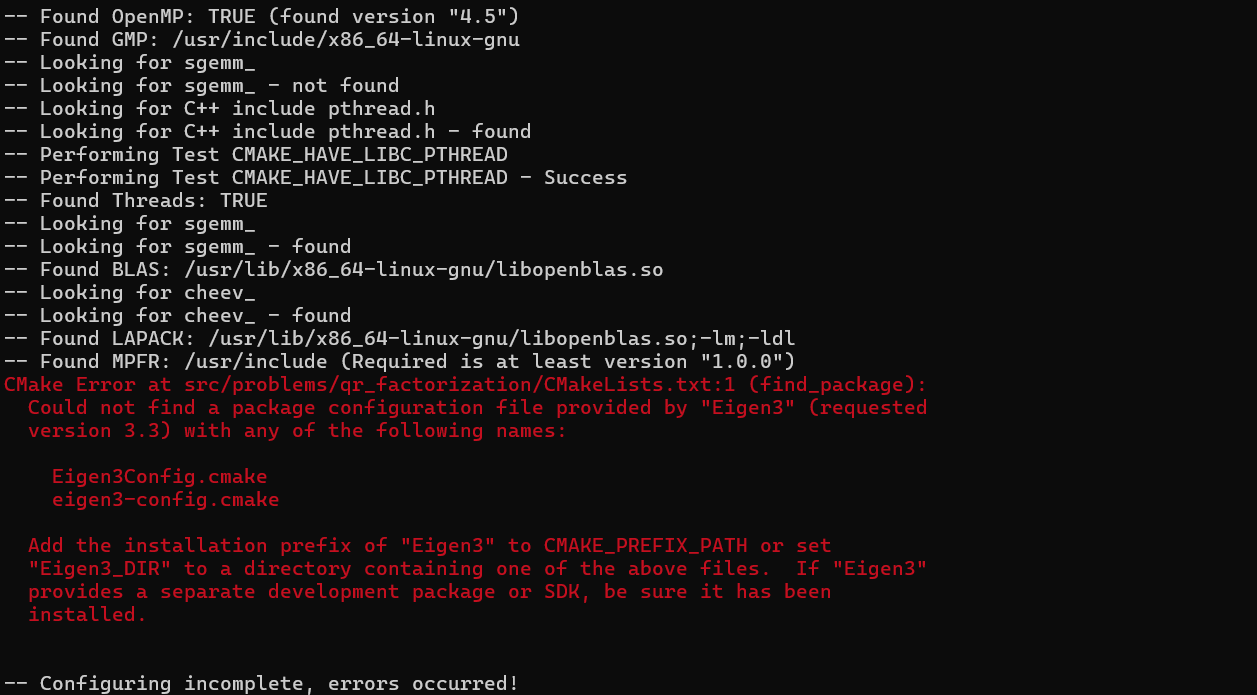
Lỗi này là do ta chưa cài Eigen, một dependency cần có để build flatter.

Tải nốt bằng lệnh sau:

sudo apt install libeigen3-dev

Rồi sau đó chạy lại toàn bộ quá trình một lần nữa

cd ~/flatter/build
cmake ..
make -j$(nproc)

Mọi người thấy thông báo như này hiện ra thì coi như oke

-- Found FPLLL: /usr/include (found suitable version "5.4.1", minimum required is "5.1.0")
-- Configuring done
-- Generating done
-- Build files have been written to: /home/duc112006/flatter/build

Cuối cùng là sao chép file thực thi vào /usr/local/bin để chạy trong VSCode

duc112006@LAPTOP-VB45ARKK:~/flatter/build$ sudo cp bin/flatter /usr/local/bin/flatter
duc112006@LAPTOP-VB45ARKK:~/flatter/build$ which flatter
/usr/local/bin/flatter
duc112006@LAPTOP-VB45ARKK:~/flatter/build$

Test:

from sage.all import *
from Crypto.Util.number import *
def flatter(M):
    import re
    from subprocess import check_output
    # compile https://github.com/keeganryan/flatter and put it in $PATH
    z = "[[" + "]\n[".join(" ".join(map(str, row)) for row in M) + "]]"
    ret = check_output(["flatter"], input=z.encode())
    return matrix(M.nrows(), M.ncols(), list(map(int, re.findall(b"-?\\d+", ret))))
M = [[-2, 2], [-2, 1]]
M = Matrix(ZZ, M) 
M = M.transpose()
M = flatter(M)
print(M)
M = [[-2, 2], [-2, 1]]
M = Matrix(ZZ, M) 
m = M.transpose()
print(m.LLL())

Lưu ý: Do thuật toán LLL thực hiện rút gọn theo cột của ma trận nên trước khi rút gọn cần phải dùng cú pháp M.transpose() để chuyển vị ma trận hoặc nếu ta đã sắp xếp đúng theo định dạng thì không cần phải chuyển vị nữa.

TODO:
Mình có thử implement lại thuật toán LLL như dưới đây:

M = Matrix([[-10 , -8 , 10 , -2],
[ -2 , -6 , -3 , -1],
[ -3,  10  ,-8 , -8],
[  1,  -2, -10,  -6]])
 
 
def toList(mat):
    return [mat[i] for i in range(mat.nrows())]
# pure python + sage matrix supporter
# M = Matrix(ZZ,[[4, 1, 7, -1],[2, 1, -3, 4], [1, 0, -2, 7], [6, 2, 9, -5]])
def gram_schmidt(mat):
    u = []
    v = toList(mat)
    n = mat.nrows()
    mu = Matrix(QQ, mat.nrows(), mat.ncols())
    n = mat.nrows()
    for i in range(n):
        vi = v[i]
        for j in range(i):
            mu[i,j] = (vi * u[j]) / (u[j]*u[j])
            vi = vi - mu[i,j] * u[j]
        u.append(vi)
    mu[0,0] = 1
    return Matrix(QQ, u), Matrix(QQ, mu)
def print_mat(mat):
    for row in mat:
        print(row,'\n')
 
_, riel = M.gram_schmidt()
_ , mu = gram_schmidt(M)
assert mu[0,0] == riel[0,0]
def my_LLL(mat, delta= 0.99):
    mat = Matrix(QQ,mat)
    ortho, mu = mat.gram_schmidt()
    k = 1
    n = ortho.nrows()
    while k < n :
        for j in range(k-1, -1,-1):
            prod = (mu[k,j])
            if abs(prod) > 1/2:
 
                mat[k] = mat[k] - round(prod)*mat[j]
                ortho , mu = mat.gram_schmidt()
        if (ortho[k].dot_product(ortho[k])) >= (delta-mu[k,k-1]**2)*(ortho[k-1].dot_product(ortho[k-1])):
            k +=1
        else:
            mat[k], mat[k-1] = mat[k-1], mat[k]
            ortho , mu = mat.gram_schmidt()
            k = max(k-1, 1)
    return mat 
 
print(flatter(M),"\n")
print(M.LLL(),"\n")
print(my_LLL(M,delta=0.99))
def compare_mat(mat1, mat2):
    if mat1.nrows() != mat2.nrows() or mat1.ncols() != mat2.ncols():
        return False
    for i in range(mat1.nrows()):
        if mat1[i] != mat2[i]:
            return False
    return True
for _ in range(100):
    M = Matrix(ZZ,[[randint(-100,100) for _ in range(5)] for _ in range(5)])
    res1 = my_LLL(M)
    res2 = M.LLL()
    if not compare_mat(res1, res2):
        print(_)
        print("Mismatch found!")
        print("Input matrix:")
        print(M)
        print("Custom LLL result:")
        print(res1)
        print("Sage LLL result:")
        print(res2)
        break
else:
    print("All tests passed!")

Và có 2 vấn đề như sau:

• Đầu tiên là trong sage, nó chạy LLL mặc định với hệ số $\delta =0.99$.
• Thứ hai là trong quá trình chạy Debug, hai ma trận res1 và res2 ra kết quả khác nhau thì thường rơi vào 2 trường hợp. Trường hợp thứ nhất là có một hàng bị đổi dấu so với LLL của sage. Trường hợp thứ hai là hàng cuối cùng của thuật toán của mình không nhỏ bằng hàng cuối cùng của sage.LLL(). Hiện tại mình vẫn chưa hiểu tại sao lại như vậy.
  Mình có tìm thêm các tài liệu khác về LLL. Một bài mà mình tìm thấy ở trên trang CryptoBook như sau: https://cryptohack.gitbook.io/cryptobook/lattices/lll-reduction/lll-reduced-basis

def LLL(B):
    d = B.nrows()
    i = 1
    while i<d:
        size_reduce(B)
        if swap_condition(B):
            i += 1
        else:
            B[i],B[i-1] = B[i-1],B[i]
            i = max(i-1,1)
    return B

Một số paper nên đọc:
[1] https://eprint.iacr.org/2025/774.pdf
[2]

Note: Kết hợp với yield
Yield là một keyword khá thú vị trong Python.

from sage.all import *
B = matrix(ZZ, [
    [1,2,3],
    [4,5,6],
    [7,8,9]
])
print(B)
def shortest_vector(B):
    B_ = B.LLL()
    for row in B_:
        if not row.is_zero(): # method for ZZ-vector sage
            yield row
l = shortest_vector(B)
print(l.__next__())

Trong python có hai kiểu object chính đó là iterator object và generator object.
Hiểu đơn giản thì iterator object là những object mà ta có thể dùng hàm for để duyệt qua.
Còn về generator thì nó hoạt động như sau: Khi hàm shortest_vector ở trên được gọi nó sẽ trả về một generator object chứ không thực sự gọi hay thực thi hàm. Chỉ khi ta gọi ta gọi phương thức __next__ của Python thì hàm sẽ bắt đầu chạy cho tới khi gặp yield và giá trị của yield sẽ được trả về cho __next__. Chi tiết hơn về yield và generator mình sẽ trình bày trong một bài khác.

Một số định lí và tính chất

Mục đích ban đầu của thuật toán LLL là phân tích các đa thức trong $\mathbb{Q}[x]$, điều này thực hiện trong thời gian đa thức. Tuy nhiên trên đường đi, nó khôi phục một vector lưới có độ dài tối đa ${\left(\frac{2}{\sqrt{3}}\right)}^m$ lần so với vector ngắn nhất trong một số lưới $\mathcal{L}$, tức là nó có thể giải được $SV{P}_{{\left(2/\sqrt{3}\right)}^m}$ trong thời gian $O\left(n^6{\log }_{3}B\right)$ trong đó $B$ là độ dài của vector cơ sở đầu vào dài nhất.

Cụ thể ta có các định lí sau đây

Định lí 1. Cho $\mathbf{B}=\{{\mathbf{b}}_1,...,{\mathbf{b}}_n\}$ là một cơ sở lattice và ${\mathbf{B}}^{\ast }=\left\{{\mathbf{b}}_1^{\ast },...,{\mathbf{b}}_n^{\ast }\right\}$ là cơ sở sau khi trực giao hóa Gram Schmidt. Khi đó ${\lambda }_1(\mathcal{L}(\mathbf{B}))⩾\underset{i\in \{1,...,n\}}{\min }\Vert {\mathbf{b}}_i^{\ast }\Vert$.

Chứng minh.

Xét $\mathbf{x}=(x_1,...,x_n)\in {\mathbb{Z}}^n$ là vector nhỏ nhất khác 0 và vì $\mathbf{x}$ khác vector 0 cho nên tồn tại một chỉ số $j$ lớn nhất sao cho $x_j\ne 0$. Khi đó $x_i=0,\forall i>j$. Bây giờ xét điểm nguyên $\mathbf{xB}$ thì ta

$$\begin{array}{c}|⟨\mathbf{xB},{\mathbf{b}}_j^{\ast }⟩|=\mid ⟨\sum _{i=1}^n{x}_i{\mathbf{b}}_i,{\mathbf{b}}_j^{\ast }⟩|\\ =\mid \sum _{i=1}^n{x}_i⟨{\mathbf{b}}_i,{\mathbf{b}}_j^{\ast }⟩|⩾|x_j|⟨{\mathbf{b}}_j,{\mathbf{b}}_j^{\ast }⟩=|x_j|\Vert {\mathbf{b}}_j^{\ast }{\Vert }^2\end{array}$$

Mà lại có

$$\begin{array}{c}|⟨\mathbf{xB},{\mathbf{b}}_j^{\ast }⟩|⩽\Vert \mathbf{xB}\Vert \cdot \Vert {\mathbf{b}}_j^{\ast }\Vert ⟹|x_j|\cdot \Vert {\mathbf{b}}_j^{\ast }{\Vert }^2⩽\Vert \mathbf{xB}\Vert \cdot \Vert {\mathbf{b}}_j^{\ast }\Vert \\ ⟹|x_j|\cdot \Vert {\mathbf{b}}_j^{\ast }\Vert ⩽\Vert \mathbf{xB}\Vert \\ ⟹\underset{i\in \{1,...,n\}}{\min }\Vert {\mathbf{b}}_i^{\ast }\Vert ⩽\Vert \mathbf{xB}\Vert \end{array}$$

Định lí 2. Cho $\mathbf{B}=\{{\mathbf{b}}_1,...,{\mathbf{b}}_n\}$ là một cơ sở rút gọn $\delta -LLL$ rút gọn. Khi đó $\Vert {\mathbf{b}}_1\Vert ⩽{\left(\frac{2}{\sqrt{4\delta -1}}\right)}^{n-1}{\lambda }_1$.

Định lí này có ý nghĩa rằng: vector đầu tiên sau khi rút gọn LLL chưa chắc là vector ngắn nhất nhưng nó là một vector gần với vector ngắn nhất của mạng.

Từ điều kiện rút gọn lattice ta có

$$\begin{array}{c}\left(\delta -{\mu }_{i+1,i}^2\right)\Vert {\mathbf{b}}_i^{\ast }{\Vert }^2⩽\Vert {\mathbf{b}}_{i+1}^{\ast }{\Vert }^2\end{array}$$

Mà ta có ${\mu }_{i+1,i}⩽\frac{1}{2}$ kéo theo $\left(\frac{4\delta -1}{4}\right)\Vert {\mathbf{b}}_i^{\ast }{\Vert }^2⩽{\Vert b}_{i+1}^{\ast }{\Vert }^2$

Cho nên

$$\begin{array}{c}\Vert {\mathbf{b}}_i^{\ast }{\Vert }^2⩽{\Vert b}_{i+1}^{\ast }{\Vert }^2\left(\frac{4}{4\delta -1}\right)\\ ⟹\Vert {\mathbf{b}}_1^{\ast }\Vert ⩽\Vert {\mathbf{b}}_i^{\ast }\Vert {\left(\frac{2}{\sqrt{4\delta -1}}\right)}^{i-1}\\ ⟹\Vert {\mathbf{b}}_1^{\ast }\Vert ⩽\Vert {\mathbf{b}}_n^{\ast }\Vert {\left(\frac{2}{\sqrt{4\delta -1}}\right)}^{n-1}\end{array}$$

Ngoài ra ta còn có một khái niệm khác gọi là heuristic. Heuristic là các giả định dùng để ước lượng số lượng vector mà lattice có trong một miền nhất định. Hai phương pháp heuristic thường được sử dụng là Gaussian Heuristic và Geometric Series Assumption GSA.
Mọi người có thể xem qua bài viết sau: LLL on the Average. Tác giả có đưa ra một nhận xét như sau:
Giả thuyết: Với mỗi lưới ngẫu nhiên $\mathcal{L}$ có rank là $n$ và cho $b_1,...,b_n$ là một cơ sở rút gọn LLL của nó. Thì khi đó

$$\Vert b_i\Vert ⩽\sqrt{i}(1.02{)}^n\det (L{)}^{1/n}$$

Gaussian Heuristic là một ước lượng của ${\lambda }_1(\mathcal{L})$: Mật đố của các điểm là $1/\det (\mathcal{L})$ , vì vậy trong một quả cầu có bán kính là $r$, chúng ta mong đợi sẽ có $v_n\times r^n/\det (\mathcal{L})$ các điểm lưới, trong đó $v_n$ là thể tính của quả cầu đơn vị $n$ chiều. Cụ thể, điều này đưa ra một ước lượng cho ${\lambda }_1$ thông qua $v_n{\lambda }_1^n/\det (\mathcal{L})\approx 1$. Vì thể tích của quả cầu đơn vị được tính bởi

$$v_n\approx \frac{1}{\sqrt{2n\pi }}{\left(\frac{2\pi e}{n}\right)}^{n/2}$$

GH đưa giả ra định:

$${\lambda }_1\approx \det (\mathcal{L}{)}^{1/n}\sqrt{\frac{n}{2\pi e}}$$

Bài toán CVP

Như đã trình bày ở trên thì thuật toán LLL giúp ta giải bài toán SVP và apprSVP. Bài toán tiếp theo mà ta tìm hiểu sẽ là bài toán CVP và apprCVP tức là bài toán tìm vector gần nhất với vector cho trước. Cụ thể với lưới $\mathcal{L}$ và một target vector $t$, ta sẽ tìm $v\in \mathcal{L}$ sao cho $\Vert v-t\Vert$ là nhỏ nhất.

Thuật toán Babai

Đầu tiên để sinh ra một cơ sở thuận tiện cho tính toán thì ta cần làm 2 việc đó là rút gọn LLL cho cơ sở và chuyển cơ sở thành cơ sở trực giao với thuật toán gram schmidt. Chẳng hạn với cơ sở trực giao $\mathbf{B}=\{{\mathbf{b}}_1,...,{\mathbf{b}}_n\}$ thì độ dài của mỗi vector trong $\mathcal{L}(\mathbf{B})$ được tính bởi

$$\begin{array}{c}\Vert a_1{\mathbf{b}}_1+...+a_n{\mathbf{b}}_n{\Vert }^2=a_1^2\Vert {\mathbf{b}}_1{\Vert }^2+...+a_n^2\Vert {\mathbf{b}}_n{\Vert }^2\end{array}$$

Ta xét một siêu phẳng sinh bởi $n-1$ vectors đầu tiên của lưới và đặt $t^{\prime }=t-c_n{b}_n$ trong đó $c_n$ là số nguyên được chọn sao cho siêu phẳng được tịnh tiến bởi $c_n{\mathbf{b}}_n$ gần $t$ nhất có thể. $c_n$ sẽ được tính bởi $c_n=\lfloor \frac{⟨\mathbf{b},{\mathbf{b}}_n^{\ast }⟩}{⟨{\mathbf{b}}_n^{\ast },{\mathbf{b}}_n^{\ast }⟩}\rfloor$. Tiếp tục làm tương tự cho tới khi thu được tổng $c_i{\mathbf{b}}_i$ và cũng chính là giá trị mà ta cần tìm.

Định nghĩa siêu phẳng: Tập $X$ là siêu phẳng trong ${\mathbb{R}}^n$ nếu $X$ là không gian affine $n-1$ chiều.

Chi tiêt mọi người có thể xem ở đây https://ecampusontario.pressbooks.pub/daisotuyentinh/chapter/hyperplanes-and-half-spaces/

Implement:

from sage.all import *
from sage.modules.free_module_integer import IntegerLattice
def flatter(M):
    import re
    from subprocess import check_output
    # compile https://github.com/keeganryan/flatter and put it in $PATH
    z = "[[" + "]\n[".join(" ".join(map(str, row)) for row in M) + "]]"
    ret = check_output(["flatter"], input=z.encode())
    return matrix(M.nrows(), M.ncols(), list(map(int, re.findall(b"-?\\d+", ret))))
 
def Babai_CVP(mat,target):
    M = flatter(mat)
    G = M.gram_schmidt()[0]
    diff = target 
    for i in reversed(range(G.nrows())):
        diff -= M[i] * ((diff*G[i]) / (G[i]*G[i])).round()
    return target - diff 

Kannan’s Embedding

Một cách khác để xử lí CVP đó là nhúng vector cần tính vào trong ma trận cơ sở của lưới và chuyển từ bài CVP thành SVP.

Xét $\mathbf{B}=\{{\mathbf{b}}_1,...,{\mathbf{b}}_n\}$ là cơ sở của lưới và $\mathbf{t}=(t_1,...,t_n)$ là target vector. Nghiệm của CVP lúc này sẽ có dạng $c_1{\mathbf{b}}_1+...+c_n{\mathbf{b}}_n$. Như vậy

$$\begin{array}{c}\mathbf{t}\approx \sum _{i=1}^n{c}_i{\mathbf{b}}_i\\ ⟹\mathbf{t}=\sum _{i=1}^n{c}_i{\mathbf{b}}_i+e\\ ⟹\mathbf{t}=\mathbf{xB}+e\end{array}$$

trong đó ta có thể coi $e$ là sai số nhỏ. Xét một lưới $(n+1)\times (n+1)$ với các cơ sở như sau:

$$\begin{array}{c}{\mathbf{B}}^{\prime }=\left[\begin{array}{cc}\mathbf{B}& 0\\ \mathbf{t}& q\end{array}\right]\end{array}$$

Viết đầy đủ ma trận ra như sau:

$$\begin{array}{c}{\mathbf{B}}^{\prime }=\left[\begin{array}{ccccc}{b}_{11}& b_{12}& \cdots & b_{1n}& 0\\ b_{21}& b_{22}& \cdots & b_{2n}& 0\\ ⋮& ⋮& \ddots & ⋮& ⋮\\ b_{n1}& b_{n2}& \cdots & b_{nn}& 0\\ t_1& t_2& \cdots & t_n& q\end{array}\right]\end{array}$$

Như vậy lưới này sẽ có một vector nhỏ $(e,q)=(e_1,e_2,...,e_n,q)$ sinh bởi tổ hợp tuyến tính $(-c_1,...,-c_n,1)$.

Ví dụ:

Giả sử ta có một ma trận như sau:

$$\begin{array}{c}B=\left(\begin{array}{ccc}35& 72& -100\\ -10& 0& -25\\ -20& -279& 678\end{array}\right)\end{array}$$

là một lattice trong ${\mathbb{R}}^3$. Vector mục tiêu của ta là $w=(100,100,100)$. Ta chọn trọng số $q=1$. Xây dựng ma trận mới và làm theo thuật toán ở trên:

$$\begin{array}{c}{B}^{\prime }=\left(\begin{array}{cccc}35& 72& -100& 0\\ -10& 0& -25& 0\\ -20& -279& 678& 0\\ 100& 100& 100& 1\end{array}\right)\end{array}$$

M = Matrix(ZZ, [[35,72,-100,0],[-10,0,-25,0],[-20,-279,678,0],[100,100,100,1]])
target = vector(ZZ,[100,100,100])
M = flatter(M)
print(M)
for row in M:
    if row[-1] == 1:
        vec = target - vector(row[:-1])
        print(f"solution là {vec}")

Bài toán ACD

Cho các tham số $\gamma ,\eta ,\rho$ và $p$ là một số nguyên lẻ có độ lớn là $\eta$-bit. Như vậy ta sẽ có

$$2^{\eta -1}<p<2^{\eta }$$

$p$ không nhất thiết phải là số nguyên tố và ta sẽ xem xét kĩ hơn trong các biến thể khác của bài toán. Ta xét một tập hợp các mẫu thử như sau:

$${\mathcal{D}}_{\gamma ,\rho }(p)=\left\{pq+r|q\leftarrow \mathbb{Z}\cap \left[0,2^{\gamma }/p\right),r\leftarrow \mathbb{Z}\cap \left(-2^{\rho },2^{\rho }\right)\right\}$$

Trên thực tế ta có giá trị của $\rho$ nhỏ hơn $\eta$ rất nhiều cho nên các mẫu thử từ ${\mathcal{D}}_{\gamma ,\rho }(p)$ sẽ gồm các số $x_i<2^{\gamma }$ với xác suất lớn. Hơn nữa với $t$ đủ lớn và $x_1,...,x_t$ là các mẫu thử từ ${\mathcal{D}}_{\gamma ,\rho }(p)$ thì ta kì vọng rằng sẽ có ít nhất một giá trị $x_i$ sao cho

$$\begin{array}{c}{2}^{\gamma -1}<x_i<2^{\gamma }\end{array}$$

Lúc này bài toán ACD được phát biểu như sau: Cho một số hữu hạn các giá trị được làm nhiễu $x_i$ từ ${\mathcal{D}}_{\gamma ,\rho }(p)$, hãy tính toán lại giá trị của $p$.

Một biến thể của bài là bài PACD - partial approximate common divisor problem: Tương tự bài ACD nhưng ta được biết được một mẫu “sạch” không bị làm nhiễu là $x_0=p{q}_0$
Ngoài ra ta còn có các decisional versions của bài nhưng trong phạm của bài viết này mình sẽ không đề cập đến (nếu có mình sẽ viết lại trong thư mục Theoretical Cryptography)

Ngoài ra còn một phiên bản khác là CRT-ACD mọi người có thể xem tại đây

Tóm lại, bài toán ACD với tham số $(\gamma ,\eta ,\rho )$ là bài toán tìm lại giá trị bí mật $p$ từ một tập mẫu thử có dạng $x_i=p{q}_i+r_i$ trong đó

• $p$ có độ lớn $\eta$ bits,
• các số $r_i$ được phân bố đều trong khoảng $[-2^{\rho }+1,2^{\rho }-1]\cap \mathbb{Z}$
• các số $q_i$ được phân bố đều trong khoảng $[0,2^{\gamma -\eta }]\cap \mathbb{Z}$

Simultaneous Diophantine approximation - SDA

Attack này được dùng trong trường hợp giá trị làm nhiễu quá lớn để có thể vét cạn và ta có nhiều mẫu bị nhiễu. Tức là các giá trị $r_i$ lớn và ta được biết nhiều giá trị $x_i$.
Ý tưởng chính của attack này đó là từ phương trình $x_i=p{q}_i+r_i$ với $1\le i\le t$ thì ta có thể viết lại dưới dạng:

$$\frac{x_i}{x_0}\approx \frac{q_i}{q_0}$$

với mỗi $1\le i\le t$. Ta có thể xem $\frac{q_i}{q_0}$ như một xấp xỉ Diophante của $\frac{x_i}{x_0}$. Như vậy nếu như ta xác định được giá trị của $\frac{q_i}{q_0}$ thì ta có thể giải được bài toán ACD bằng cách tính $r_0\equiv x_0(\mathrm{mod}{q}_0)$ và có $(x_0-r_0)/q_0=p$. Thực tế ta không cần giá trị của mẫu $x_0=p{q}_0$ để giải bài toán trên.
Ta sẽ xây dựng một lattice $\mathbb{B}$ có rank là $t+1$ như sau:

$$\mathbb{B}=\left(\begin{array}{ccccc}{2}^{\rho +1}& x_1& x_2& \dots & x_t\\ & -x_0& -x_0& & \\ & & -x_0& & \\ & & & \ddots & \\ & & & & -x_0\end{array}\right)$$

Nó sẽ chứa một vector $\mathbf{v}$ là tổ hợp tuyến tính của $(q_0,q_1,...,q_t)$ như sau:

$$\begin{array}{c}\mathbf{v}=(q_0,q_1,...,q_t)\mathbb{B}\\ =\left(2^{\rho +1}{q}_0,q_0{x}_1-q_1{x}_0,...,q_0{x}_t-q_t{x}_0\right)\\ =\left(q_0{2}^{\rho +1},q_0{r}_1-q_1{r}_0,...,q_0{r}_t-q_t{r}_0\right)\end{array}$$

Vì ta có : với cặp $x_i=p{q}_i+r_i,x_j=p{q}_j+r_j$ thì

$$\begin{array}{c}{q}_i=(x_i-r_i)/p\\ ⟹q_i{x}_j=(x_i-r_i)x_j/p\\ q_j=(x_j-r_j)/p\\ ⟹q_j{x}_i=(x_j-r_j)x_i/p\\ ⟹q_i{x}_j-q_j{x}_i=\frac{x_i{x}_j-r_i{x}_j-x_i{x}_j+x_i{r}_j}{p}=\frac{x_i{r}_j-r_i{x}_j}{p}\end{array}$$

Mặt khác

$$\begin{array}{c}{q}_i{r}_j=(x_i-r_i)r_j/p\\ q_j{r}_i=(x_j-r_j)r_i/p\\ ⟹q_i{r}_j-q_j{r}_i=(x_i{r}_j-x_j{r}_i)/p\end{array}$$

Vì $q_i\approx 2^{\gamma -\eta }$ cho nên chuẩn euclid (norm) của $\mathbf{v}$ sẽ xấp xỉ $\sqrt{t+1}\times 2^{\gamma -\eta +\rho +1}$

Bây giờ đối với ma trận $\mathbb{B}$ của ta thì theo Gaussian Heuristic ở trên, nếu như

$$\begin{array}{c}\sqrt{t+1}\times 2^{\gamma -\eta +\rho +1}<\sqrt{\frac{t+1}{2\pi e}}\det (L{)}^{1/(t+1)}\end{array}$$

thì ta có thể kì vọng vector $\mathbf{v}$ sẽ là vector ngắn nhất sinh ra bởi lưới. Như vậy ta sẽ chạy thuật toán LLL cho lưới trên và lấy phần tử $\mathbf{w}$ đầu tiên của vector kết quả chia cho $2^{\rho +1}$. Đây chính là giá trị có thể có của $q_0$. Sau đó ta sẽ tính $r_0\equiv x_0(\mathrm{mod}{q}_0)$ và kiểm tra giá trị của $p=(x_0-r_0)/q_0$ bằng cách tính thử xem $x_i\mathrm{mod}p$ có “nhỏ” hay không.
Implement:

from sage.all import *
def flatter(M):
    from subprocess import check_output
    from re import findall
    z = "[[" + "]\n[".join(" ".join(map(str, row)) for row in M) + "]]"
    ret = check_output(["flatter"], input=z.encode())
    return matrix(M.nrows(), M.ncols(), map(int, findall(b"-?\\d+", ret)))
def symmetric_mod(x, m):
    return int((x + m + m // 2) % m) - int(m // 2)
def SDA(x, rho):
    assert len(x) >= 2
    R = 2 ** (rho + 1)
    B = matrix(ZZ, len(x), len(x))
    B[0, 0] = R
    for i in range(1, len(x)):
        B[0, i] = x[i]
        B[i, i] = -x[0]
    B_ = flatter(B)   
    for v in B_:
        if v[0] != 0 and v[0] % R == 0:
            q0 = v[0] // R
            r0 = symmetric_mod(x[0], q0)
            p = abs((x[0] - r0) // q0)
            r = [symmetric_mod(xi, p) for xi in x]
            if all(-R < ri < R for ri in r):
                return int(p), r

(Nếu k có flatter thì mọi người có thể dùng LLL của sage =)) mà flatter lâu lâu cx hay lỏ,mn nên thử cả hai và nên cập nhật phiên bản mới của flatter trước khi chạy)

Hidden Number Problem - HNP

Có hai phiên bản khác nhau của HNP, ở đây mình sẽ trình bày lại phiên bản quen thuộc hơn. Phiên bản còn lại mọi người có thể xem ở đây

Hidden Number Problem. Cho $p$ là một số nguyên tố và $\alpha \in [1,p-1]$ là một số nguyên bí mật mà ta cần tìm với điều kiện rằng ta được biết $m$ cặp giá trị $\{(t_i,a_i){\}}_{i=1}^m$ thỏa mãn

$$\begin{array}{c}{\beta }_i-t_i\alpha +a_i=0\mathrm{mod}p\end{array}$$

trong đó các giá trị ${\beta }_i$ được ẩn đi và ta chỉ biết rằng $|{\beta }_i|<B$ với $B<p$ nào đó.
Có hai hướng tiếp cận đó là dựa vào bài toán CVP hoặc SVP.

Đối với thiết lập CVP, ta sẽ xét lattice được xây dựng dựa trên ma trận sau:

$$\begin{array}{c}\mathbf{B}=\left[\begin{array}{ccccc}p& & & & \\ & p& & & \\ & & \ddots & & \\ & & & p& \\ t_1& t_2& \dots & t_m& 1/p\end{array}\right]\end{array}$$

Ta viết lại phương trình HNP dưới dạng ${\beta }_i+a_i=t_1\alpha +k_{i}p$ với mỗi số nguyên $k_i$. Như vậy ta có một vector $({\beta }_1+a_1,...,{\beta }_m+a_m,\alpha /p)$ được sinh ra bởi tổ hợp tổ tuyến $\mathbf{x}=(k_1,...,k_m,\alpha )$. Đặt $\mathbf{t}=(a_1,...,a_m,0)$ và $\mathbf{u}=({\beta }_1,...,{\beta }_m,\alpha /p)$ thì ta có $\mathbf{xB}-\mathbf{t}=\mathbf{u}$ trong đó độ dài của $\mathbf{u}$ (norm) bị chặn trên bởi $\sqrt{m+1}B$ trong khi định thức của $\mathbf{B}$ là $p^{m-1}$. Như vậy ta sẽ chuyển sang bài toán CVP với target vector là $\mathbf{t}$. Để khôi phục lại $\alpha$ ta sẽ thử nhân phần tử cuối của vector với $p$.

Còn đối với SVP, thì ta sẽ xét lattice sinh bởi ma trận sau đây:

$$\begin{array}{c}\mathbf{B}=\left[\begin{array}{cccccc}p& & & & & \\ & p& & & & \\ & & \ddots & & & \\ & & & p& & \\ t_1& t_2& \dots & t_m& B/p& \\ a_1& a_2& \dots & a_m& & B\end{array}\right]\end{array}$$

Lattice này sẽ chứa một vector ngắn là

$$\begin{array}{c}{\mathbf{u}}^{\prime }=({\beta }_1,...,{\beta }_m,\alpha B/p,-B)\end{array}$$

sinh bởi tổ hợp tuyến tính $(k_1,...,k_m,\alpha ,-1)$. Ta có $\Vert {\mathbf{u}}^{\prime }\Vert <\sqrt{m+2}B$ và dựa vào các giả định ở trên về cơ sở rút gọn LLL thì ta có thể kì vọng rằng sẽ tìm được vector ${\mathbf{u}}^{\prime }$ trong số các cơ sở của ma trận mới. Lưu ý thêm rằng, lattice này cũng chứa một vector ngắn là $(0,...,0,B,0)$, sinh bởi $(-t_1,...,-t_m,p,0)$ cho nên ${\mathbf{u}}^{\prime }$ có thể rơi vào vector ngắn thứ hai của cơ sở (hoặc nếu không thì ta có thể thử hết =))?)

def hnp(p, T, A, B, lattice_reduction=None, verbose=False):
    r"""
    Returns the solution of the given hidden number problem instance. i.e. finds
    `\alpha \in [1, p - 1]` satisfying
 
    .. MATH::
 
        \beta_i - t_i \alpha + a_i \equiv 0 \pmod p
 
    where the `t_i` and `a_i` are given by ``T`` and ``A``, and the `\beta_i`
    are bounded above by ``B``.
 
    The implementation follows the algorithm as described in section 2.5 of [1].
 
    INPUT:
 
    - ``p`` -- The modulus `p` as described above.
 
    - ``T`` -- A list of integers representing the `t_i`.
 
    - ``A`` -- A list of integers representing the `a_i`.
 
    - ``B`` -- The upper bound on the `\beta_i` as described above.
 
    OUTPUT:
 
    The integer `\alpha` which is a solution to the HNP instance. If no solution
    could be found, None is returned.
 
    REFERENCES:
 
    [1] Martin R. Albrecht and Nadia Heninger. *On Bounded Distance Decoding with Predicate:
    Breaking the “Lattice Barrier” for the Hidden Number Problem.*
    In Lecture Notes in Computer Science, p. 528--558. Springer, 2021.
    https://link.springer.com/chapter/10.1007/978-3-030-77870-5_19
    """
 
    verbose = (lambda *a: print('[hnp]', *a)) if verbose else lambda *_: None
 
    if len(T) != len(A):
        raise ValueError(f'Expected number of t_i to equal number of a_i, but got {len(T)} and {len(A)}.')
 
    m = len(T)
    M = p * Matrix.identity(QQ, m)
    M = M.stack(vector(T))
    M = M.stack(vector(A))
    M = M.augment(vector([0] * m + [B / p] + [0]))
    M = M.augment(vector([0] * (m + 1) + [B]))
    M = M.dense_matrix()
 
    verbose('Lattice dimensions:', M.dimensions())
    lattice_reduction_timer = cputime()
    if lattice_reduction:
        M = lattice_reduction(M)
    else:
        M = M.LLL()
    verbose(f'Lattice reduction took {cputime(lattice_reduction_timer):.3f}s')
 
    for row in M:
        if row[-1] == -B:
            alpha = (row[-2] * p / B) % p
            if all((beta - t * alpha + a) % p == 0 for beta, t, a in zip(row[:m], T, A)):
                return alpha
        if row[-1] == B:
            alpha = (-row[-2] * p / B) % p
            if all((beta - t * alpha + a) % p == 0 for beta, t, a in zip(-row[:m], T, A)):
                return alpha
 
    return None
 

Extended Hidden Number Problem - EHNP

EHNP là một biến thể mở rộng của HNP. Cụ thể bài toán được phát biểu như sau:
Extended Hidden Number Problem. Cho $p$ là một số nguyên tố và $x\in [1,p-1]$ là một số nguyên bí mật thỏa mãn:

$$x=\overline{x}+\sum _{j=1}^m{2}^{{\pi }_j}{x}_j$$

trong đó ta biết giá trị của $\overline{x}$ và ${\pi }_j$, và các số nguyên $x_j$ thỏa mãn $0⩽x_j<2^{v_j}$ (ta không được biết $x_j$) với $v_j$ cho trước. Bây giờ giả sử ta có $d$ phương trình dưới dạng

$$\begin{array}{c}{\alpha }_i\sum _{j=1}^m{2}^{{\pi }_j}{x}_j+\sum _{j=1}^{l_i}{\rho }_{i,j}{k}_{i,j}={\beta }_i-{\alpha }_i\overline{x}(\mathrm{mod}p)\end{array}$$

với $1⩽i⩽d$ và ${\alpha }_i\ne 0(\mathrm{mod}p),{\rho }_{i,j}$ và ${\beta }_i$ được biết giá trị. Hơn nữa các giá trị $k_{i,j}$ bị chặn bởi $0⩽k_{i,j}<2^{{\mu }_{i,j}}$ và ta không biết giá trị của các số này. Bài toán của ta sẽ là tìm cách khôi phục lại giá trị $x$ từ các phương trình trên.
Như vậy, một trường hợp cho bài EHNP sẽ là:

$$\begin{array}{c}\left(\overline{x},p,\{{\pi }_j,v_j{\}}_{j=1}^m,{\left\{{\alpha }_i,\{{\rho }_{i,j},{\mu }_{i,j}{\}}_{j=1}^{l_i},{\beta }_i\right\}}_{i=1}^d\right)\end{array}$$

Mọi người để ý rằng ta chỉ biết khoảng chặn của các giá trị bị ẩn, nói đơn giản chính là độ lớn về bit của các số này.

Giải các phương trình tuyến tính

Tiếp theo ta sẽ tìm hiểu xem thuật toán LLL có ứng dụng gì trong việc giải các phương trình tuyến tính.
Ví dụ 1. Xét phương trình

$$3x+5y=2$$

Ta muốn tìm một cặp nghiệm nhỏ $(x,y)$. Một ý tưởng đơn giản là tìm cách xây dựng một lattice sao cho $(x,y)$ cũng là một vector được sinh bởi lattice này.
Ta viết lại phương trình như sau:

$$3x+5y-2k=0$$

Và dựng một ma trận có dạng :

$$\begin{array}{c}(x,y,-k)\left(\begin{array}{ccc}1& & 3\\ & 1& 5\\ & & -2\end{array}\right)=(x,y,0)\end{array}$$

Ta kì vọng $(x,y,0)$ sẽ là vector ngắn của lattice này.
Sau khi rút gọn ta được:

sage: M = Matrix([[1,0,3],[0,1,5],[0,0,-2]])
sage: M.LLL()
[-1  1  0]
[ 0 -1 -1]
[-1  0  1]
sage:

Ta chú ý tới các vector nào có phần tử cuối cùng là 0 thì đây chính là vector mà ta cần tìm. Như vậy ta có được một nghiệm là $(-1,1)$. Thử lại:

$$-3+5=2$$

Nhưng cách build này có một vấn đề đó là ta không kiểm soát được giá trị của $k$. Như vậy sẽ có khả năng trong một số trường hợp ta tìm ra một vector đúng định dạng mà ta mong muốn nhưng giá trị $k$ lại không thỏa mãn bằng $1$ khiến cho phương trình vô nghiệm.
Một cách xử lí khác đó là dựng ma trận

$$\begin{array}{c}(a,b,c)\left(\begin{array}{cccc}1& & & 3\\ & 1& & 5\\ & & 1& -2\end{array}\right)=(a,b,c,3a+5b-2c)\end{array}$$

Bây giờ mình thử xài LLL cho ma trận này xem sao và cố tìm một vector ngắn trong cơ sở rút gọn có dạng $(...,...,1,0)$. Đối với trường hợp này mình có được ngay:

sage: M = identity_matrix(3).augment(vector([3,5,2]))
sage: M
[1 0 0 3]
[0 1 0 5]
[0 0 1 2]
sage: M.LLL()
[ 1 -1  1  0]
[-1  0  1 -1]
[ 0  0  1  2]

Như vậy trong trường hợp này thì ta có một nghiệm $(a,b,c)=(1,-1,1)$.
Nhưng không phải trong trường hợp nào thì thuật toán LLL cũng hoạt động tốt.
Chẳng hạn ta có một phản ví dụ sau đây:
Xét phương trình

$$33x+7y=11$$

Mình thử với ma trận:

$$\begin{array}{c}(x,y,k)\left(\begin{array}{ccc}1& & 33\\ & 1& 7\\ & & -11\end{array}\right)=(x,y,0)\end{array}$$

sage: M = Matrix([[1,0,33],[0,1,7],[0,0,-11]])
sage: M.LLL()
[-1  0  0]
[ 0 -3  1]
[ 0 -2 -3]
sage:

Thì không thu được hàng nào cho kết quả như mong muốn. Mình thử luôn với cách xây dựng ma trận kia xem sao:

$$(x,y,k)\left(\begin{array}{cccc}1& & & 33\\ & 1& & 7\\ & & 1& -11\end{array}\right)=(x,y,k,0)$$

sage: M = identity_matrix(3).augment(vector([33,7,-11]))
sage: M.LLL()
[-1  0 -3  0]
[ 1 -3  1  1]
[ 0 -2 -1 -3]
sage: M
[  1   0   0  33]
[  0   1   0   7]
[  0   0   1 -11]
sage:

Có 1 hàng có dạng $(-1,0,-3,0)$. Mình thay lại thì được: $-1\times 33+0\times 7=-3\times 11$. Mặc dù phương trình thỏa mãn VT = VP nhưng đây không phải là nghiệm ta mong muốn vì ta cần $k=1$.

Để giải quyết việc này thì mình sẽ đánh “trọng số” vào hàng chứa hệ số của $k$, tức là hàng thứ 3.
Sau khi chạy thì mọi người thấy ở hàng thứ 3 số $1000$ vẫn giữ nguyên, điều này chứng tỏ $k=1$.

sage: M = identity_matrix(3).augment(vector([33,7,-11]))
sage: M[2,2] = 1000
sage: M.LLL()
[   1   -5    0   -2]
[   1   -4    0    5]
[   1   -3 1000    1]
sage:

Theo cách mình hiểu cho việc đặt hệ số như trên đó là nằm ở cách LLL hoạt động. Ở mỗi bước nó sẽ kiểm tra điều kiện dưới đây:

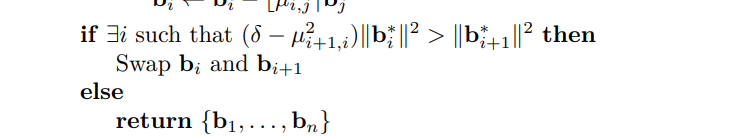
Tức là nếu như có một hàng $\Vert {\mathbf{b}}_{i+1}^{\ast }\Vert$ có chuẩn (norm) đủ lớn thì nó sẽ bỏ qua và chỉ tính toán đúng 1 lần.
Nhưng rất tiết là, với cách làm trên ta không thu lại được nghiệm cho phương trình ban đầu vì phần tử cuối của vector trên lại khác 0, trong khi ta lại mong muốn nó phải bằng 0.

Để làm được điều này thì ta sẽ nhân cột cuối cùng của ma trận với một số rất lớn khác. Như vậy, khi LLL chạy , nó sẽ cố gắng tìm một vector ngắn theo chuẩn Euclid và vì các vector của ta trong cơ sở ban đầu đều khá lớn cho nên nó sẽ bỏ qua các vector mà có phần tử cuối cùng khác 0 và cố gắng tìm một vector có phần tử cuối cùng bằng 0 (lưu ý rằng ta chỉ đang kì vọng rằng sẽ có một vector như vậy vì LLL không phải lúc nào cũng có thể cho ta nghiệm chính xác được)

sage: M = identity_matrix(3).augment(vector([33,7,-11]))
sage: M[2,2] = 1000
sage: M[:,-1] *= 1000
sage: M
[     1      0      0  33000]
[     0      1      0   7000]
[     0      0   1000 -11000]
sage: M.LLL()
[   7  -33    0    0]
[   3  -14    0 1000]
[  -2   11 1000    0]
sage:

Như vậy ta đã tìm được một nghiệm cho phương trình đó là $(x,y,k)=(-2,11,1)$.
Tiếp tục ta sẽ tìm hiểu một số phiên bản khác của bài toán giải phương trình/hệ phương trình tuyến tính

Phương trình đồng dư tuyến tính

Trong trường hợp ta muốn giải các phương trình đồng dư có dạng:

$$3x+5y-2=0\mathrm{mod}3$$

Ta sẽ chuyển về dạng phương trình tuyến tính như trên bằng việc thêm hệ số của modulo vào. Cụ thể

$$3x+5y-2+3k=0$$

Xét lattice sau:

$$(x,y,z,k)\left(\begin{array}{cccc}1& & & 3\\ & 1& & 5\\ & & 1& -2\\ & & 0& 3\end{array}\right)=(x,y,z,0)$$

Bước tiếp theo là đánh trọng số cho phù hợp.
Ta muốn $z=1$ nên sẽ lấy cột số 3 nhân với trọng số $W$ và ta cũng muốn entry cuối cùng của target vector bằng 0 nên ta nhân cột cuối cùng của lattice với trọng số $W$.

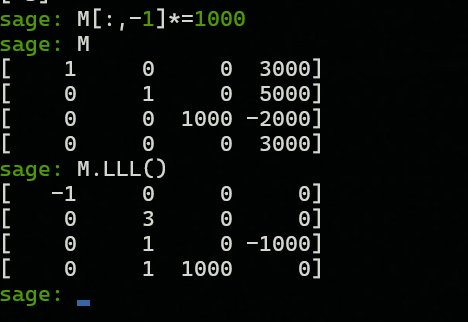
Một nghiệm là $(0,1)$ ở hàng cuối cùng.

CTF Challenges

Một số bài CTF có ứng dụng Lattice trong lời giải.

IdekCTF 2025 - Diamond Ticket

Source code của bài:

from Crypto.Util.number import *
 
#Some magic from Willy Wonka
p = 170829625398370252501980763763988409583
a = 164164878498114882034745803752027154293
b = 125172356708896457197207880391835698381
 
def chocolate_generator(m:int) -> int:
    return (pow(a, m, p) + pow(b, m, p)) % p
 
#The diamond ticket is hiding inside chocolate
diamond_ticket = open("flag.txt", "rb").read()
assert len(diamond_ticket) == 26
assert diamond_ticket[:5] == b"idek{"
assert diamond_ticket[-1:] == b"}"
diamond_ticket = bytes_to_long(diamond_ticket[5:-1])
flag_chocolate = chocolate_generator(diamond_ticket)
chocolate_bag = []
 
#Willy Wonka are making chocolates
for i in range(1337):
    chocolate_bag.append(getRandomRange(1, p))
 
#And he put the golden ticket at the end
chocolate_bag.append(flag_chocolate)
 
#Augustus ate lots of chocolates, but he can't eat all cuz he is full now :D
remain = chocolate_bag[-5:]
 
#Compress all remain chocolates into one
remain_bytes = b"".join([c.to_bytes(p.bit_length()//8, "big") for c in remain])
 
#The last chocolate is too important, so Willy Wonka did magic again
P = getPrime(512)
Q = getPrime(512)
N = P * Q
e = bytes_to_long(b"idek{this_is_a_fake_flag_lolol}")
d = pow(e, -1, (P - 1) * (Q - 1))
c1 = pow(bytes_to_long(remain_bytes), e, N)
c2 = pow(bytes_to_long(remain_bytes), 2, N) # A small gift
 
#How can you get it ?
print(f"{N = }")
print(f"{c1 = }")
print(f"{c2 = }") 
 
# N = 85494791395295332945307239533692379607357839212287019473638934253301452108522067416218735796494842928689545564411909493378925446256067741352255455231566967041733698260315140928382934156213563527493360928094724419798812564716724034316384416100417243844799045176599197680353109658153148874265234750977838548867
# c1 = 27062074196834458670191422120857456217979308440332928563784961101978948466368298802765973020349433121726736536899260504828388992133435359919764627760887966221328744451867771955587357887373143789000307996739905387064272569624412963289163997701702446706106089751532607059085577031825157942847678226256408018301
# c2 = 30493926769307279620402715377825804330944677680927170388776891152831425786788516825687413453427866619728035923364764078434617853754697076732657422609080720944160407383110441379382589644898380399280520469116924641442283645426172683945640914810778133226061767682464112690072473051344933447823488551784450844649

Phân tích: Đầu tiên ta có 3 tham số $p,a,b$ và hàm chocolate_generator(m). Nó sẽ nhận vào số mũ $m$ và trả về $a^m+b^m\mathrm{mod}p$.

Tiếp theo cách flag được mã hóa trong bài này như sau:

diamond_ticket = open("flag.txt", "rb").read()
assert len(diamond_ticket) == 26
assert diamond_ticket[:5] == b"idek{"
assert diamond_ticket[-1:] == b"}"
diamond_ticket = bytes_to_long(diamond_ticket[5:-1])
flag_chocolate = chocolate_generator(diamond_ticket)

flag_chocolate chính là $a^{flag}+b^{flag}\mathrm{mod}p$. Và ta phải giải để tìm lại flag từ thông tin này.

for i in range(1337):
    chocolate_bag.append(getRandomRange(1, p))

Hàm này tạo một danh sách chocolate_bag gồm các số ngẫu nhiên trong khoảng $[1,p]$ nhưng sau đó chỉ lấy 5 số cuối trong đó bao gồm flag của ta.

chocolate_bag.append(flag_chocolate)
#Augustus ate lots of chocolates, but he can't eat all cuz he is full now :D
remain = chocolate_bag[-5:]

Sau đó nó sẽ nối các phần tử trong remain lại và mã hóa bằng RSA

remain_bytes = b"".join([c.to_bytes(p.bit_length()//8, "big") for c in remain])
 
#The last chocolate is too important, so Willy Wonka did magic again
P = getPrime(512)
Q = getPrime(512)
N = P * Q
e = bytes_to_long(b"idek{this_is_a_fake_flag_lolol}")
d = pow(e, -1, (P - 1) * (Q - 1))
c1 = pow(bytes_to_long(remain_bytes), e, N)
c2 = pow(bytes_to_long(remain_bytes), 2, N) # A small gift

Trước tiên mình cần tìm lại remain_bytes từ hai giá trị $c1$ và $c2$.

$$\begin{array}{l}{c}_1=m^e\mathrm{mod}N\\ c_2=m^2\mathrm{mod}N\end{array}$$

Với $e$ được tạo bởi e = bytes_to_long(b"idek{this_is_a_fake_flag_lolol}") là một số lẻ.
Bây giờ giả sử ta có $c_1=m^a$ và $c_2=m^b$. Muốn tính lại $m$ ta sẽ làm như sau: Ta gọi $g=\gcd (a,b)$. Đối với bài này thì $g=1$. Như vậy theo định lí Bezout tồn tại $u,v$ để $au+bv=1$.

Sau đó ta sẽ tính $c_1^u=m^{au}$ và $c_2^v=m^{vb}$ và tính $c_1^u\times c_2^v=m^{au+vb}=m$ và khôi phục lại được giá trị của $m$ ban đầu. Nếu như $g>1$ thì ta có thể lấy nth_root(g) của nó .

Script cho bước này:

from Crypto.Util.number import *
from sage.all import *
 
 
N = 85494791395295332945307239533692379607357839212287019473638934253301452108522067416218735796494842928689545564411909493378925446256067741352255455231566967041733698260315140928382934156213563527493360928094724419798812564716724034316384416100417243844799045176599197680353109658153148874265234750977838548867
c1 = 27062074196834458670191422120857456217979308440332928563784961101978948466368298802765973020349433121726736536899260504828388992133435359919764627760887966221328744451867771955587357887373143789000307996739905387064272569624412963289163997701702446706106089751532607059085577031825157942847678226256408018301
c2 = 30493926769307279620402715377825804330944677680927170388776891152831425786788516825687413453427866619728035923364764078434617853754697076732657422609080720944160407383110441379382589644898380399280520469116924641442283645426172683945640914810778133226061767682464112690072473051344933447823488551784450844649
e = bytes_to_long(b"idek{this_is_a_fake_flag_lolol}")
def attack(n, e1, c1, e2, c2):
    g, u, v = xgcd(e1, e2)
    p1 = pow(c1, u, n) if u > 0 else pow(pow(c1, -1, n), -u, n)
    p2 = pow(c2, v, n) if v > 0 else pow(pow(c2, -1, n), -v, n)
    return int(ZZ(int(p1 * p2) % n).nth_root(g))
remain_bytes = attack(N,e,c1,2,c2)
print(remain_bytes)

remain_bytes có len == 80 bytes được tạo thành từ 5 phần, mỗi phần 16 bytes chính là len của số nguyên tố p. Vậy ta tách nó thành 5 phần bằng nhau và lấy phần cuối chính là flag_chocolate của ta.

print(remain_bytes)
remain_bytes = long_to_bytes(remain_bytes)
print(len(remain_bytes))
remain = [
    int.from_bytes(remain_bytes[i:i + 16], "big")
    for i in range(0, 80, 16)
]
flag_chocolate = remain[-1]
print(flag_chocolate)
# 99584795316725433978492646071734128819

Tiếp theo ta sẽ giải DLP.
Bây giờ ta có $p,a,b$ và $a^m+b^m\mathrm{mod}p$.
Kiểm tra order:

sage: p = 170829625398370252501980763763988409583
sage: factor(p-1)
2 * 40841 * 50119 * 51193 * 55823 * 57809 * 61991 * 63097 * 64577
sage:

Order của nhóm khá smooth.

Nhưng ta cần tìm order của hai số $a$ và $b$.

sage: p = 170829625398370252501980763763988409583
....: a = 164164878498114882034745803752027154293
....: b = 125172356708896457197207880391835698381
sage: K = Zmod(p)
sage: a = K(a)
sage: b = K(b)
sage: print(a.multiplicative_order())
85414812699185126250990381881994204791
sage: print(b.multiplicative_order())
85414812699185126250990381881994204791
sage: order1 = a.multiplicative_order()
sage: order2 = a.multiplicative_order()
sage: assert order1 == order2
sage: order = p-1
sage: print(order/order1)
2
sage:

Vậy cấp của $a$ và $b$ là $(p-1)/2$.
Về cơ bản thì không thể giải được bài toán nếu như giữ nguyên cả hai số $a$ và $b$ được. Nên mình đã thử tìm một số $k$ sao cho $b=a^k\mathrm{mod}p$ coi sao.

sage: k  = discrete_log(b,a,order1)
sage: print(k)
73331
sage:

Đưa về bài toán $a^m+a^{km}\mathrm{mod}p$.

Bây giờ mình muốn tìm lại $a^m$ nên đã thử dựng đa thức $f=x+x^k-c$.

Vấn đề là số mũ $k$ khá lớn nên để tìm lại nghiệm khá tốn thời gian nên mình xài một trick lỏ học được sau giải MaltaCTF vừa rồi. https://github.com/ctf-mt/maltactf-2025-quals/blob/master/crypto/grammar-nazi/solution/solve.sage

Ta đã biết với $K$ là một trường hữu hạn có đặc số nguyên tố $p$ thì $x^{p^n}-x=x\prod _{u_i\in K^{\ast }}(x-u_i)$ với $K^{\ast }=K\backslash \{0\}$.

Ở đây ta đang làm việc với $K=GF(p)$ và một nhóm con của nó là nhóm các thặng dư bậc hai vì bậc của $a$ là $(p-1)/2$. Nhóm con của một nhóm cyclic cũng là một nhóm cyclic cho nên mình sẽ dựng một đa thức khác là $g=x^r-x$ trong đó $r=(p-1)/2+1$.

Vấn đề là trong sage khi gọi $g$ như vậy thì gặp lỗi

OverflowError: cannot fit 'int' into an index-sized integer

Do số mũ quá lớn nên sage không xử lí được. Để khắc phục thì mình lấy f.gcd(pow(x,r,f)-x).roots(multiplicities=False) là được.

K = Zmod(p)
a = K(a)
b = K(b)
order1 = a.multiplicative_order()
order2 = b.multiplicative_order()
r = (p-1)//2 + 1
print(order1 ,'\n')
print(order2)
# a^m + b^m = c mod p 
k = discrete_log(b,a)
# k = 73331
c = K(flag_chocolate)
P = PolynomialRing(K, 'a')
x = P.gen()
f = x  + x**k - c 
res = f.gcd(pow(x,r,f)-x).roots(multiplicities=False)
print(res)
# 126961729658296101306560858021273501485

a_m = K(126961729658296101306560858021273501485)
m0 = discrete_log(a_m,a,order1)
# m0 = 4807895356063327854843653048517090061

Bước tiếp theo là tìm lại $m$ ban đầu. Ta biết $a^m=a^{m_0}\mathrm{mod}p$ thì $m\equiv m_0\mathrm{mod}order$. Vấn đề là $m0$ chỉ có 122 bits trong khi $m$ gốc ban đầu có gồm 20 bytes tức là 160 bits ??

Ở bước này thì mình tham khảo Writeup của một bài trong giải SEETF 2023

Ứng dụng vào bài: Từ đề bài ta biết được flag có độ dài 26 bytes nhưng bằng việc bỏ đi 6 kí tự thì nó chỉ còn 20 bytes. Giả sử ban đầu flag của ta là $a=a_{19}{a}_{18}....a_0$ thì sau khi chuyển từ bytes thành long (mặc định hàm bytes_to_long của pycryptodome lấy theo big endian ) nó sẽ có giá trị là:

$$\begin{array}{c}m=\sum _{i=0}^{19}a[0]\times 256^{20-i-1}\end{array}$$

Bây giờ ta có $r\equiv m\mathrm{mod}\left(\frac{p-1}{2}\right)$ vừa tìm được chính là tổng trên nhưng được lấy theo modulo $\frac{p-1}{2}$. Như vậy

$$\begin{array}{c}\sum _{i=0}^{19}a[0]\times 256^{20-i-1}\equiv r\left(\mathrm{mod}\frac{p-1}{2}\right)\\ ⟹\sum _{i=0}^{19}a[0]\times 256^{20-i-1}-r+k\frac{p-1}{2}=0\end{array}$$

Ta có thể build một lattice có dạng như sau:

$$\begin{array}{c}(a_{19},a_{18},...,a_0,1,k)\left(\begin{array}{ccccccc}1& & & & & 0& 256^{19}\\ & 1& & & & 0& 256^{18}\\ & & 1& & & 0& 256^{17}\\ & & & \ddots & & ⋮& ⋮\\ & & & & 1& 0& 256^0\\ & & & & & -1& -r\\ & & & & & 0& (p-1)//2\end{array}\right)=(a_{19},a_{18},...,a_0,-1,0)\end{array}$$

Và kì vọng vector $(a_{19},a_{18},...,a_0,-1,0)$ là vector ngắn nhất sinh ra bởi lưới.
Nếu để nguyên ma trận như vậy rồi rút gọn LLL thì sẽ không ra được kết quả như mong muốn. Do vậy ta cần chỉnh lại các hệ số trong ma trận một chút.
Như đã làm ở trên trong phần ứng dụng giải hệ phương trình tuyến tính, thì bây giờ ta muốn tạo một cơ sở cho lattice mà sau khi rút gọn LLL sẽ sinh ra một vector có dạng $(a_{19},a_{18},...,-1,0)$. Thì đầu tiên để cho phần tử cuối cùng của Vector này bằng 0 thì ta cần scale cột cuối cùng của ma trận bằng một số lớn. Ở đây mình chọn scale hệ số là $10^6$.

Tiếp theo mình sẽ ép các entries trong các vector của cơ sở về một biên cụ thể, ở đây vì $a_i$ đều là các kí tự ASCII nên mình sẽ lấy hàng gần cuối có dạng $(-a,-a,...,-a,-1,-m)$. Giá trị $a$ này mình sẽ brute force để tìm ra sau =)) đại loại thì nó sẽ từ $[80,126]$.

Tiếp theo là làm sao để phần tử kế cuối bằng $-1$. Thì mục tiêu của ta là scale cột thứ 2, nhưng vấn đề là scale như thế nào? Thì lúc này ta vẫn sẽ scale cột gần cuối bởi một số lớn bất kì nào đó. Nếu như sau khi LLL, giá trị tuyệt đối của cột đó vẫn giữ nguyên thì coi như ta thành công. Chẳng hạn ta đánh trọng số vào cột gần cuối là $W$ thì ta sẽ kì vọng thu được một vector có dạng:

$$(a_{19},a_{18},...,a_0,-W,0)$$

Còn về việc chọn trong số bao nhiêu cho hợp lí thì mình bruteforce thôi. Trước tiên thì mình chạy thử $W\in [100,1000]$ coi sao.
Một số lưu ý khác trong việc chọn weight và các kĩ thuật giải quyết tương tự mình sẽ note vào trong các ví dụ khác. Còn đối với bài này thì cách bruteforce như trên vẫn đủ để giải quyết.

Final solve script:

from sage.all import *
from Crypto.Util.number import *
 
 
# step 1
N = 85494791395295332945307239533692379607357839212287019473638934253301452108522067416218735796494842928689545564411909493378925446256067741352255455231566967041733698260315140928382934156213563527493360928094724419798812564716724034316384416100417243844799045176599197680353109658153148874265234750977838548867
c1 = 27062074196834458670191422120857456217979308440332928563784961101978948466368298802765973020349433121726736536899260504828388992133435359919764627760887966221328744451867771955587357887373143789000307996739905387064272569624412963289163997701702446706106089751532607059085577031825157942847678226256408018301
c2 = 30493926769307279620402715377825804330944677680927170388776891152831425786788516825687413453427866619728035923364764078434617853754697076732657422609080720944160407383110441379382589644898380399280520469116924641442283645426172683945640914810778133226061767682464112690072473051344933447823488551784450844649
 
e = bytes_to_long(b"idek{this_is_a_fake_flag_lolol}")
g, u, v = xgcd(e,2) # return eu + 2v = 1
# c1 = m^e mod N
# c2 = m^2 mod N
p1 = pow(c1, u, N) if u > 0 else pow(pow(c1,-1,N), -u, N)
p2 = pow(c2, v, N) if v > 0 else pow(pow(c2,-1,N), -v, N)
c = (p1*p2) % N
remain_bytes = int((ZZ(c)).nth_root(g))
# print(remain_bytes)
remain = long_to_bytes(remain_bytes)
# print(len(remain))
chunk = [remain[i*16:(i+1)*16] for i in range(5)]
flag_chocolate = int(bytes_to_long(chunk[-1]))
# print(flag_chocolate)
 
# step 2
p = 170829625398370252501980763763988409583
a = 164164878498114882034745803752027154293
b = 125172356708896457197207880391835698381
K = GF(p)
# flag_chocolate = a^m + b^m mod p 
a = K(a)
b = K(b)
choco = K(99584795316725433978492646071734128819)
# print(a.multiplicative_order())
# print((p-1)//2)
k = b.log(a)
# print(k)
# a^m + (a^m)^k = choco
R = PolynomialRing(K, 'x')
x = R.gen()
f = x + x**k - choco
r = (p-1)//2 + 1 
# root = f.gcd(pow(x,r,f)-x).roots(multiplicities = False)
# print(len(root))
# for r in root:
#     print(r)
 
a_pow_m = K(126961729658296101306560858021273501485)
# m = discrete_log(a_pow_m,a, operation='*', ord = (p-1)//2)
# print(m)
m = 4807895356063327854843653048517090061
 
# step 3
# m = bytes_to_long(flag[5:-1]) % (p-1)//2 
 
 
 
modulus = GF(p)(a).multiplicative_order()
for aa in range(80,126):
    M = (identity_matrix(20).augment(vector([0]*20)).augment(vector([256**i for i in range(19,-1,-1)]))
     .stack(vector([-aa]*20+[-1,-m])).stack(vector([0]*20+[0,-modulus]))
)
    M[:,-1] *= 10**6
    cand = []
    for i in range(100,1000): # precomputed
        M_ = copy(M)
        M_[:,-2] *= i
        cand.append(M_)
    for Mat in cand:
        for row in Mat.LLL():
            if row[-1] != 0:
                continue
            if row[-2] == i:
                row *= -1
            if row[-2] == -i:
                try:
                    flag = b"idek{" +bytes([val+ aa for val in row[:-2]]) + b"}"
                    print(flag)
                    break
                except:
                    continue

Flag: b'idek{tks_f0r_ur_t1ck3t_xD}'
Note: Trong sage thì để copy 2 ma trận ta sẽ dùng cú pháp copy(M). Lưu ý là không được gán kiểu M_ = M vì thực chất lúc này M_ và M sẽ trỏ vào chung một object nên khi M_ thay đổi thì M cũng thay đổi theo.

sage: M = [1,2]
sage: M_ = M
sage: M_.append(3)
sage: M_
[1, 2, 3]
sage: M
[1, 2, 3]
sage:

Bigger RSA - ICTF 2025

Source code của bài:

from Crypto.Util.number import getPrime, bytes_to_long
import secrets
 
n = 32
e = 0x10001
N = 64
 
flag = b'ictf{REDACTED}'
flag = secrets.token_bytes((n * 63) - len(flag)) + flag
 
ps = [getPrime(512) for _ in range(n)]
 
m = 1
for i in ps:
    m *= i
 
nums = [CRT([1 + secrets.randbits(260) for _ in range(n)],ps) for __ in range(N)]
ct = pow(bytes_to_long(flag),e,m)
print(f"ct={ct}")
print(f"m={m}")
print(f"nums={nums}")

Tóm tắt
Flag ban đầu được padding thêm với độ dài là $32\times 64$
Tiếp theo ta có $ps=(p_1,...,p_{32})$ là danh sách 32 số nguyên tố 512 bits và modulo $m=\prod p_i$
nums là danh sách gồm kết quả các lần lấy CRT giữa $ps$ và một danh sách gồm các số nguyên ngẫu nhiên 260 bits.
Mỗi số như vậy, ta kí hiệu $n_k$, và nó thỏa mãn

$$n_k=CRT([r_k],[ps])$$

$r_k$ là một danh sách, hay một vector có độ dài là $n$ và được sinh ngẫu nhiên. Có 64 số $n_k$ như vậy.
Cuối cùng, flag của ta được mã hóa bởi $c=f^e\mathrm{mod}m$ và như mọi bài RSA khác ta cần tính được $d$ hoặc factor được $m$ để khôi phục lại được flag.

Ta thử biến đổi một chút giả thiết xem có gì đặc biệt hay không. Đầu tiên thì

$$n_k\equiv r_{k,i}\mathrm{mod}{p}_i$$

với mỗi số nguyên tố thứ $i$ trong danh sách còn $r_{k,i}$ là phần tử thứ $i$ trong vector $r_k=(r_{k,1},...,r_{k,n})$
Để ý là $r_{k,i}$ chỉ có độ lớn 260 bits so với các số nguyên tố $p_i$ là 512 bits. Vậy có gì sus ở đây? Đó là số samples $n_k$ lớn hơn số lượng số nguyên tố. Hơn nữa các giá trị $r_{k,i}$ lại quá bé so với $p_i$.

Bây giờ, lấy $p$ là một ước nguyên tố bất kì của $m$. Ta có thể viết lại thành bài toán ACD như sau:
Với mỗi $n_i$ thì

$$\begin{array}{l}{n}_i\mathrm{mod}p=r_i\\ \to n_i=q_{i}p+r_i\end{array}$$

Trong đó $k_i$ là dương. Như vậy $n_i$ là các samples, $p$ là số nguyên tố cần tìm, $r_i$ là các giá trị nhiễu.
Ta còn được biết thêm $m=q_{0}p$ cho nên bài toán trở thành bài toán PACD.
Ta xét ma trận cơ sở sau cho lattice:

$$\begin{array}{c}\left(\begin{array}{cccc}{2}^{\rho }& n_1& \dots & n_t\\ & -m& & \\ & & \ddots & \\ & & & -m\end{array}\right)\end{array}$$

Tham khảo paper sau: https://eprint.iacr.org/2024/1125
Thì ta sẽ có một target vector là $(2^{\rho },q{r}_1,q{r}_2,...,q{r}_t)$

Script:

from sage.all import *
from Crypto.Util.number import *
import sys
 
sys.set_int_max_str_digits(10000)
with open('out.txt', 'r') as f:
    data = f.read()
exec(data)
 
nums = [int(x) for x in nums]
 
 
div = [12825661825870628850035560085682551683599110773726524106705997668244622779138663874897188475532877346205351955798732755558280092764135146502129333667531273,8849247080017422968286437560856142727623460763416403577915666822178621608829806605500730083192464088951638255609862020842573930004233720962540782545280917,12636179557635617452330128900423408842203389165865121860715801777216229507326731176068378415443505580234827587398680217811961679156951468691902900103283911,11665745491363584588817758173385553841468540459223034134224520669080487519540459517215245489433604657499780082512713663950711196057044379146579277447799641,10193210740767481473019618865757332045483969049172119373119467546501386913192524524088772310971356251443648842033224837315650991716119025633640697531018367,9860624430169179237101055140804005926260705273640679771060493754118380693166065551828723961325454473971232083913340785881413212684328745162716466341641703,8198765300403592826995984598440010099299153959564583088450304003994567588524986967140022948908468461503336165216389379643683563868592309564288732696196381,9399262846686720121315011141246648648055720745589751334250006699346316301281406786164502055605005070307260703436205524531442672416733277454751993628239631,7497205738581146511103214896532677970457601649900731236571252220143900638616771482674225243713240678251231847312424134189997058636723535861317763367633641,7289439242613403106913459953533062235438046592580050161223546293986062672239122190117370418630708553308438056766522682658538319102870922735502285582346747,12124606354540998387639696647514778171390523966240573154197017585530097111120368848520582154389803842482131244622368481712191458586181046555572124506613251,8105728567181529459394712985955452977924319583512637598854476013170561450113469084263200652258026471761829210987135826986745819766196980387074523097073657,6888700314385525292891778504743903584494529201288456809897688611641727120314651838233357514470910140534188619131620158693746771631555477899637441167477453]
div.append(7726570664077541569500609696487048853838858832232316686907006156699125589812818999760924082971861995437404863431384702397077467392233847841327356802363801)
div.append(8294044843320375342348440529265349310074336151926255303163456989874771309684232815646857160747968956263444065889923214458311650834127524874020718004703063)
div.append(8687188077388195197942412743119551152103076903384085416686479408856483000564526371547623206120647931153257229436717458717575895261026293921157873579347523)
div.append(8490624530961994264444272185306408329363711421693856030812478451335188077181280975487946465857547173006542435443423976275834896724688227217926575962445513)
div.append(9541198062644681818808906411342123600626696583059201220221791584990253737970206989008003268135201906569392496774193646464956405331120128112399213831516337)
div.append(9642162115840667658352928012612798175019852945876463189055031372099012909214031198954415788761783119020007723644518732724519301404234194296600021095310903)
div.append(11066225255954538956086391741274699004347741181044658117167199042247926550120819890539271565072220049729624283496671856280507820187174258310798768129809643)
div.append(10650706826079171733657402315658310046544484471219755815725148141088338415583895923747381442625886083665772937180335995318006736797238782810674274323124133)
div.append(6785761235506713513312376605068746300508567988972967034908692130737909162277214242079951731490834338699742346610832568248780644781764595342608460247910481)
div.append(8407275141814496946434929131996618204666441620022963349926711447735636663875635640548596520101748747468751119077417845036475579129094075130130034331680921)
div.append(13304120223798684507299474307520334491371996458244395318574383542629544993743450154833532639719767107951453068991436133689433290741347655241089642756940277)
div.append(10055208163312818248211905302258271244505754955239681522022788361513189069056199757860548713346899425633159936306160990941381990616768347250997679669878983)
div.append(12988817382193630091431137466820689413789500172268375590891549414964355529275662477376343028415637353009995758639222386125419322028291397443311373577470303)
div.append(10367349082240332209527336924610925419601094897177737276881325800532431393521161527661162528033983877369208872297487119704934757865447474657206102635334471)
div.append(11440156453910579361669220291235374570309164955514078974773040600050290240145655916509977706026037945264964523845742593392070913039518343805824343520807021)
div.append(8952377250397141807169471340795003194902515693028612379693700708755894948874509812090273788737686410835319935781937173371830062801823355403555607449768299)
div.append(11252209285465510687668877327220225314043368189496350631539299840601500088579688774183851797307134519221926482312227783088020515669175292851103664879859359)
div.append(6732242136158511160127027152866595392289544303661945940690114485462693735083507892072393100603357914889898547391329909425237179853498580999515276757335323)
div.append(6884631120492254742857384566667440506378312675186188443493248024590755198358479687940627103876640032346648673787841382544028198056732915127377326737365661)
assert all(is_prime(x) for x in div)
print(len(div))
m = int(m)
for p in div:
    assert m % p == 0
    # m //= p
 
# LLL ở đây:
# rho = 260
# t = 64
# M = Matrix(ZZ, t+1, t+1)
# while len(div)<32:
#     print("hiện tại tìm được :", len(div))
#     M[0,0] = 2**rho
#     for i in range(1,t+1):
#         M[0,i] = nums[i-1]
#         M[i,i] = -m 
#     M =    M.LLL()
#     found = False
#     for r in M:
#         if r[0] % 2**rho == 0:
#             q = gcd(int(r[0]//(2**rho)),m)
#             p = m//q
#             if is_prime(p):
#                 assert m % p == 0 
#                 print("tìm thêm được 1 ước nguyên tố:", p)
#                 div.append(p)
#                 m//=p      
phi = 1 
for ps in div:
    phi *= (ps-1)
d = int(pow(int(0x10001),-1,int(phi)))
flag = long_to_bytes(pow(int(ct),int(d),int(m)))
print(flag)

Flag:

ictf{rsa_lattices_and_crt_in_1_challenge_surely_has_real_world_applications_lmao_8719617206370154061234128157781624678026841512064124}

NOTE: Trong quá trình làm bài này có một chỗ khiến mình khá ức chế đó là LLL không cho ra hết được tất cả các ước trong cùng 1 lần chạy. Nếu bị kẹt ở một ước mãi không chạy ra thì mọi người thử xáo trộn lại danh sách các ước nguyên tố div rồi chạy thêm một lần nữa xem sao. Mình phải thêm bớt một chút cái danh sách div rồi chia lại cho m cỡ vài lần nó mới ra (???)

RSARSA - ICTF Round 52

Source code của bài:

from secret import flag
from Crypto.Util.number import bytes_to_long, getPrime
from os import urandom
 
p, q, P, Q = 1, 1, 1, 1
while p%3 == 1: p = getPrime(1001)
while q%3 == 1: q = getPrime(1001)
while P%3 == 1: P = getPrime(1024)
while Q%3 == 1: Q = getPrime(1024)
 
n = p*q
N = P*Q
 
m = bytes_to_long(flag.encode() + urandom(250-len(flag)))
e = 3
 
c = pow(m,e,n)
C = (pow(p,e,N)*q)%N
 
with open('out.txt','w') as file:
    file.write(f'{n = }\\n')
    file.write(f'{c = }\\n')
    file.write(f'{N = }\\n')
    file.write(f'{C = }\\n')
 
'''
n = 236165963974549843165116395504697902191713379536628118224442456369682302266394059291805550850454501790983078745877277808465242450967192483721221804260097540207577805062483656523327027127554710603966355779002569448126827875849586909708264874355346913072634179303036432164732044525075631421114547665911909245396864649081324916352615048804238378500443339490430805687717735684234839495464001575301049381927288871113238709183695134250935765261299598697578849137375656662373462784922948497996422774555641898913228531573884546030084889237337034678567704892293682351242487623366576639394595575585737748297628969
c = 70937012742384298918498947273158135897378405817961054208468507698675885078698256087375111837428304573078062065633783770628342991758025350342481268180700230612722899026588541878904025893741429507151056686887872849449670311554735563584135338155830845926213289013822577616362794865255147852918994796746331323556683930502366845200103692080775988066038363189731329287562177600843653604176315077351590599271405298532429144976167210974674215140921019287905291182057378400248332045718636113089603523143042785670709665781815838353423684587315486764254364359269569359888642641186171777475467206816292957014109298
N = 13559643931510231890645252059392928830324878403065777432078047001203751827960606291671049295745925572045928516195747933143730424354729124065331936456182264578676144427400292605461916569434409294456724314100819999479249740665646695282083306225220537019377541170020872360049287615554093874460563300874852415511897525645607710048718121342471391046511248087651223041929052149218448630378746909560110882899655656687984011210519333987281129803478797350285596913131043564417404130060868808451206852147929161483360924558387919617786314342462258102165618528861476250258876654302439406603504196138731002715669914240460335010891
C = 8275456195949033635467084095519107709201520788369843769112612900914126045121100567953979244052722913960259224583894825296560682673296622047075175324016507276388107904876439908187727967560228110789357765846667845045209064071847259841181338077835834748735605960343420564692832127030070311244168918947119031684158691819391344400702542409477570193678230185099108849985093513086193902773249508226511128276263713550182135750315888219451287568184957554794890731479934946953654922694958015237442372049821287406228796371974841586661090969263065535555883597103891939136230373286602239899758144274469967582717851587584634595648
'''

Đầu tiên bài cho 4 số $p,q,P,Q$ trong đó $p,q$ có độ lớn 1001 bits còn $P,Q$ thì có độ lớn 1024 bits. Ta được biết thêm thông tin về $C=p^{e}q\mathrm{mod}N=p^{3}q\mathrm{mod}N$. Ở đây là mod $N$ chứ không phải mod $n$ nếu không thì $C=0$. Bây giờ ta có thể biến đổi

$$n^2{C}^{-1}\mathrm{mod}N\leftrightarrow p^2{q}^2{p}^{-3}{q}^{-1}=p^{-1}q\mathrm{mod}N$$

Từ đây, đặt $t=p^{-1}q\mathrm{mod}N$ thì ta có

$$tp-q=kN$$

Có thể chuyển về lattice để tính

$$p\times (t,1)+(-k)\times (N,0)=(q,p)$$

Target vector của ta sẽ là $(q,p)$. Vector này có norm là $\sqrt{p^2+q^2}\sim 2^{1001}$ trong khi đó các cơ sở của lưới có độ lớn khoảng $2^{2000}$ cho nên ta có thể kì vọng hàng đầu tiên sau khi rút gọn sẽ chứa $q$.

Script:

from Crypto.Util.number import *
from sage.all import *
from sage.modules.free_module_integer import IntegerLattice
n = 
c = 
N = 
C = 
t = (n*n*pow(C,-1,N)) % N
M = Matrix([[t,1],[N,0]]).LLL()
for row in M:
    print(row,'\\n')
for row in M:
    if gcd(row[0],n) > 1 :
        q = ZZ(int(abs(row[0])))
        print(abs(row[0]))
p = n//int(q)
phi = (p-1)*(q-1)
d = pow(3,-1,phi)
m = pow(int(c),int(d),int(n))
print(long_to_bytes(int(m)))
# b'ictf{my_d0u813D_RSA_D!D_n07_Cook}

Hệ mật LWE

Trước tiên ta nhắc lại bài toán học với lỗi - Learning With Errrors problem. Bài toán học với lỗi là bài toán yêu cầu ta khôi phục lại một giá trị bí mật $s\in {\mathbb{Z}}_q^n$ bằng việc cho biết một dãy các phương trình tuyến tính xấp xỉ theo $s$. Chẳng hạn

$$\begin{array}{c}14s_1+15s_2+5s_3+2s_4\approx 8(\mathrm{mod}17)\\ 13s_1+14s_2+14s_3+6s_4\approx 16(\mathrm{mod}17)\\ 6s_1+10s_2+13s_3+1s_4\approx 3(\mathrm{mod}17)\\ ⋮\\ 6s_1+7s_2+16s_3+2s_4\approx 3(\mathrm{mod}17)\end{array}$$

Ý tưởng cơ bản của bài toán là như trên. Nhưng ta cần một định nghĩa chính xác hơn cho nó như sau

Bài toán học với lỗi. Cho $n,m,q$ là các số nguyên và $\chi$ là phân bố trên $\mathbb{Z}$. Với $s{\leftarrow }_{\chi }{\mathbb{Z}}_q^n$ có các phần tử được chọn theo phân bố $\chi$, định nghĩa ${\mathcal{D}}_{s,\chi }$ là phân bố lấy các mẫu $a\leftarrow {\mathbb{Z}}_q^n$ và $e{\leftarrow }_{\chi }\mathbb{Z}$ rồi trả về $a,⟨a,s⟩+e\in {\mathbb{Z}}_q^n\times {\mathbb{Z}}_q$.

• Với $n,q⩾2$ và $m$ mẫu độc lập từ phân bố ${\mathcal{D}}_{s,\chi }$, bài toán search LWE là bài toán tìm $s$.
• Với $n,q⩾2$ và $m$ mẫu độc lập $(a_i,b_i)$, bài toán LWE quyết định (decisional LWE problem) là bài toán phân biệt với $i=1,2,...,m$ thì $(a_i,b_i)\leftarrow \left({\mathbb{Z}}_q^n\times Z_q\right)$ hay $(a_i,b_i)\leftarrow {\mathcal{D}}_{s,\chi }$.
  Trong đó phân phối của lỗi (errors $e$) thường là phân phối Gauss (gaussian distribution) hoặc phân phối đều (uniform sampling).

Private Key Encryption from LWE

Từ ý tưởng trên ta có thể xây dựng một hệ mật như sau:
Một hệ mật khóa bí mật (private-key encryption) sẽ bao gồm 3 thuật toán chính. Đầu tiên là một thuật toán sinh khóa ngẫu nhiên $Gen$ với đầu vào là security parameter $\lambda$ và sinh ra một khóa bí mật $sk$. Tiếp theo là thuật toán mã hóa $Enc$ với đầu vào là cặp bản rõ - khóa bí mật $(m,sk)$ và output ra ciphertext $c$. Cuối cùng là thuật toán giải mã $Dec$ với đầu vào là $(c,sk)$ và output ra bản rõ ban đầu.
Cả 3 phải đảm bảo tính chất correctness tức là với mỗi key $sk$ được sinh ra bởi $Gen$ thì

$$Dec(sk,Enc(sk,m))=m$$

Thuật toán diễn ra như sau:

• KeyGen $Gen(1^{\lambda })$: Tính $n=n(\lambda ),q=q(\lambda ),\chi =\chi (\lambda )$ và khóa bí mật sẽ là

$$sk=s\leftarrow {\mathbb{Z}}_q^n$$

là một vector có độ dài là $n$ trên ${\mathbb{Z}}_q$.

• Encryption $Enc(sk,m)$: Message space của ta sẽ là $\mathcal{M}=\{0,1\}$. Mỗi messages sẽ được chuyển về dạng bit và mã hóa từng bit. Ciphertext cho message $m$ sẽ là

$$c=(a,b)=(a,s^{T}a+e+m\lfloor q/2\rceil \mathrm{mod}q)$$

trong đó $a\leftarrow {\mathbb{Z}}_q^n$ và $e\leftarrow \chi$

• Decryption $Dec(sk,c=(a,b))$: Output 0 nếu như

$$|b-s^{T}a\mathrm{mod}q|<q/4$$

ngược lại output 1.

Dual lattice Attack

Nhắc lại: Mỗi lưới $\mathcal{L}$ có một lưới đối ngẫu (dual lattice), kí hiệu ${\mathcal{L}}^{\ast }=\left\{\mathbf{w}\in {\mathbb{R}}^m|⟨\mathbf{w},\mathbf{x}⟩\in \mathbb{Z},\forall \mathbf{x}\in \mathcal{L}\right\}$.
Nói cách khác, một lưới đối ngẫu của lưới $\mathcal{L}$ là tập hợp các điểm trong không gian sinh bởi $\mathcal{L}$ sao cho tích trong của nó với bất kì điểm nào trong $\mathcal{L}$ cũng là một số nguyên.
Trên thực tế, ta sẽ tìm cách khôi phục lại giá trị bí mật $s\in {\mathbb{Z}}_q^n$ từ nhiều cặp giá trị $(a_i,b_i)$. Trong đó

$$\begin{array}{l}{a}_i\in {\mathbb{Z}}_q^n\\ b_i\in {\mathbb{Z}}_q\\ s\in {\mathbb{Z}}_q^n\end{array}$$

Các bộ số này sẽ được gom thành một ma trận và viết lại dưới dạng hệ phương trình tuyến tính $As+e=b$ trên modulo $q$, trong đó $A$ có các hàng là các vector $a_i$, $b$ là một vector cột mà mỗi entry là các giá trị $b_i$. Tương tự với $e$.

Xét một dual lattice được scaled bởi $q$ như sau:

$$q{\Lambda }^{\ast }=\{x\in {\mathbb{Z}}^m\mid x\cdot A\equiv 0\mathrm{mod}q\}$$

Bài toán giải tìm một vector ngắn trong $q{\Lambda }^{\ast }$ tương đương với giải bài toán SIS (Shortest Integer Solution) trong lattice $A$.
Bài toán SIS là bài toán được phát biểu như sau:
SIS. Cho $q\in \mathbb{Z}$ và ma trận $A$. Với $t<q$, tìm một vector $y$ thỏa mãn $0<\Vert y\Vert \le t$ sao cho

$$y\cdot A\equiv 0(\mathrm{mod}q)$$

Primal Lattice Attack (uSVP)

uSVP là bài toán tìm vector nhỏ nhất và duy nhất trong lưới.
Ta sẽ dựa vào ý tưởng của bài toán này để phá hệ mật LWE.
Đầu tiên ta phát biểu lại bài toán: Với $A,c$ thỏa mãn $c=A\cdot s+e$, ta biết rằng có một vector $w$ sao cho $A\cdot w-c\mathrm{mod}q$ là nhỏ.
Nói cách khác ta xác định được rằng có một vector ngắn (target vector) trong mạng được sinh ra bởi q-ary lattice sau:

$$B=\left(\begin{array}{cc}{A}^T& 0\\ c^T& t\end{array}\right)\in {\mathbb{Z}}_q^{(n+1)\times (m+1)}$$

Giả sử error vector của ta đủ nhỏ thì ta có thể thử tìm lại nó bằng cách xét tổ hợp tuyến tính $(s|-1)B=(e|-t)\mathrm{mod}q$
Bây giờ ta sẽ đi cụ thể vào cách xây dựng lattice để giải bài toán trên.

Ta đưa ma trận $A^T$ về dạng bậc thang rút gọn $[I_{n\times n}|A^{\prime }]$ với $A^T\in {\mathbb{Z}}_q^{n\times m}$ và $m>n$.

Sau đó xây dựng một ma trận khối như sau:

$$\begin{array}{c}B=\left(\begin{array}{ccc}{I}_{n\times n}& A^{\prime }& 0\\ 0_{(m-n)\times n}& q{I}_{(m-n)\times (m-n)}& 0\\ c^t& & t\end{array}\right)\in {\mathbb{Z}}^{(m+1)\times (m+1)}\end{array}$$

Implement:

from sage.all import * 
import random 
q = 37
assert is_prime(q)
F = GF(q)
n = 5
m = n**2
A = Matrix(GF(q),m,n,lambda i,j: randint(0,q-1))
e = vector((0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 0, 0, 0, 1, 1, 0, 0, 1, 0, 0, 1, 1, 1, 0, 0),GF(q))
V = VectorSpace(GF(q),n)
S = V.random_element()
print(f"secret key={S}")
b = (A*S) + e
def flatter(M):
    import re
    from subprocess import check_output
    # compile https://github.com/keeganryan/flatter and put it in $PATH
    z = "[[" + "]\n[".join(" ".join(map(str, row)) for row in M) + "]]"
    ret = check_output(["flatter"], input=z.encode())
    return matrix(M.nrows(), M.ncols(), list(map(int, re.findall(b"-?\\d+", ret))))
def primal_attack(A,b,fll = False):
    m = A.nrows()
    n = A.ncols()
    A_ = matrix(ZZ, A.T.rref().submatrix(0,n,n,m-n))
    b_zz = [int(x) for x in b]
    I_n = identity_matrix(ZZ,n)
    qAry = q*identity_matrix(ZZ,m-n)
    zero_mn_n = zero_matrix(ZZ, m-n, n)    
    zero_n_1  = zero_matrix(ZZ, n, 1)  
    zero_mn_1 = zero_matrix(ZZ, m-n, 1)    
    c1 = matrix(ZZ, 1, n,    b_zz[:n])    
    c2 = matrix(ZZ, 1, m-n,  b_zz[n:]) 
    t  = matrix(ZZ, 1, 1, [1])
    B = block_matrix([
    [I_n,        A_,   zero_n_1],
    [zero_mn_n,  qAry,   zero_mn_1],
    [c1,c2,t]
])
    if fll == True:
        L = flatter(B)
    else:
        L = B.LLL()
    return L 
L = primal_attack(A,b, fll = True)
print(L[0][:-1] == e)
S_ = A.solve_right(b-e)
print(f"recover secret key = {S_}")

Thực hành

LWE High Bits Message

Source code của bài

# dimension
n = 64
# plaintext modulus
p = 257
# ciphertext modulus
q = 0x10001
# bound for error term
error_bound = int(floor((q/p)/2))
# message scaling factor
delta = int(round(q/p))
 
 
V = VectorSpace(GF(q), n)
S = V.random_element()
print("S = ", S, "\n")
 
m = ?
 
A = V.random_element()
error = randint(-error_bound, error_bound)
b = A * S + m * delta + error
 
print("A = ", A)
print("b = ", b)

File output.txt mọi người có thể lên trên trang của CryptoHack để theo dõi.

Phân tích bài: Đầu tiên, hệ mật dựa trên LWE mà ta vừa trình bày sẽ thực hiện mã hóa trên từng bit $0$ hoặc $1$ của plaintext còn đối với bài trên thì nó sẽ thực hiện mã khóa trên không gian plaintext lớn hơn.
Thuật toán đầy đủ của nó sẽ trông như sau:

Trong đó $\Delta =\lfloor (q/p)\rceil$.
Mình sẽ giải thích lại thuật toán trên như sau:

• Các tham số cho trước:
  • Một không gian vector có kích thước là $n$
  • Ciphertext modulo $q$
  • Plaintext modulo $p$ , đồng nghĩa với việc ta chỉ có thể mã hóa các message có kích thước nhỏ hơn $p$
  • Scaling factor $\Delta =round(q/p)$
• Key - Gen: Tương tự với hệ mật LWE truyền thống thì secret key $S$ cũng là một vector trên ${\mathbb{Z}}_q^n$ .
• Mã hóa:
  Ciphertext sẽ là một cặp giá trị $(A,b)$ với đầu vào là $m$.
  Trong đó $A$ là một phần tử ngẫu nhiên thuộc ${\mathbb{Z}}_q^n$. Error-term $e$ sẽ nằm trong khoảng $[-\Delta /2,\Delta /2]$ và $b=⟨A,S⟩+\Delta \times m+e$ .
• Giải mã:
  Để giải mã thì ta sẽ lấy $x=b-⟨A,S⟩\mathrm{mod}q$ và tính $m=round(x/\Delta )$ . Trong Python có sẵn hàm round để làm việc này:

Sau khi thực hiện phép trừ $x=b-⟨A,S⟩$ thì ta có thể coi như $x$ xấp xỉ với $\Delta \cdot m+e$ nếu như không tính thêm modulo $q$.
Khi ta chia lấy phần nguyên thì ta mong muốn có được

$$x/\Delta =m+e/\Delta$$

Với $|e|<\Delta /2$ thì $|e/\Delta |<1/2$ cho nên ta có được $m=round(x/\Delta )$.
Câu hỏi tiếp theo là tại sao ta cần phải chọn tham số thỏa mãn $\Delta \cdot m+e<q/2$

from sage.all import * 
 
 
S =  (55542, 19411, 34770, 6739, 63198, 63821, 5900, 32164, 51223, 38979, 24459, 10936, 17256, 20215, 35814, 42905, 53656, 17000, 1834, 51682, 43780, 22391, 33012, 61667, 37447, 16404, 58991, 61772, 44888, 43199, 32039, 26885, 17206, 62186, 58387, 57048, 38393, 29306, 58001, 57199, 33472, 56572, 53429, 62593, 14134, 40522, 25106, 34325, 37646, 43688, 14259, 24197, 33427, 43977, 18322, 38877, 55093, 12466, 16869, 25413, 54773, 59532, 62694, 13948) 
 
A =  (13759, 12750, 38163, 63722, 39130, 22935, 58866, 48803, 15933, 64995, 60517, 64302, 42432, 32000, 22058, 58123, 53993, 33790, 35783, 61333, 53431, 43016, 60795, 25781, 28091, 11212, 64592, 11385, 24690, 40658, 35307, 63583, 60365, 60359, 32568, 35417, 22078, 38207, 16331, 53636, 28734, 30436, 18170, 15939, 966, 48519, 41621, 36371, 41836, 4026, 33536, 57062, 52428, 59850, 476, 43354, 61614, 32243, 42518, 19733, 63464, 29357, 56039, 15013)
b =  44007
n = 64
p = 257
q = 0x10001
error_bound = int(floor((q/p)/2))
delta = int(round(q/p))
V = VectorSpace(GF(q), n)
S = V(S)
A = V(A)
x = int((b - A*S )% q)
m = int(round(x/delta))
print(m)

LWE Low Bits Message

Source code:

# dimension
n = 64
# plaintext modulus
p = 257
# ciphertext modulus
q = 0x10001
# bound for error term
error_bound = int(floor((q/p)/2))
 
 
V = VectorSpace(GF(q), n)
S = V.random_element()
print("S = ", S, "\n")
 
m = ?
 
A = V.random_element()
error = randint(-error_bound, error_bound)
b = A * S + error * p + m
 
print("A = ", A)
print("b = ", b)
 

Code giải:

from sage.all import * 
 
S =  (10082, 48747, 17960, 55638, 37012, 51876, 10128, 37750, 7608, 58952, 33296, 25463, 38900, 85, 65248, 42153, 44966, 31594, 40676, 56828, 30325, 38502, 65083, 7497, 2667, 54022, 24029, 32162, 57267, 12253, 6668, 5181, 14906, 51655, 61347, 4722, 22227, 23606, 63183, 52860, 1670, 31085, 42633, 47197, 7255, 16150, 9574, 62956, 26742, 57998, 49467, 31224, 60073, 12730, 41419, 41042, 53032, 16339, 32913, 16351, 34283, 47845, 3617, 35718) 
 
A =  (53751, 21252, 55954, 16345, 60990, 2822, 56279, 37048, 36153, 52141, 2121, 56565, 48112, 43755, 12951, 22539, 29478, 28421, 62175, 10265, 36378, 21305, 42402, 26359, 939, 60690, 1161, 65097, 34505, 19777, 29652, 42868, 49148, 38296, 31916, 25606, 18700, 12655, 35631, 64674, 29018, 21021, 14865, 40196, 14036, 40278, 37209, 35585, 34344, 33030, 285, 58536, 56121, 40899, 24262, 62326, 57433, 5765, 24456, 28859, 45170, 14799, 21567, 55484)
b =  11507
 
n = 64
p = 257
q = 0x10001
error_bound = int(floor((q/p)/2))
V = VectorSpace(GF(q), n)
A = V(A)
S = V(S)
x = b - (A*S)
def symmetric_mod(x, m):
    return int((x + m + m // 2) % m) - int(m // 2)
x = symmetric_mod(x,q)
m = int((x%p))
print(m)

From Private to Public Key LWE

Noise Free

Source code của bài:

from utils import listener
from sage.all import *
 
 
FLAG = b"crypto{????????????????????????}"
 
# dimension
n = 64
# plaintext modulus
p = 257
# ciphertext modulus
q = 0x10001
 
V = VectorSpace(GF(q), n)
S = V.random_element()
 
def encrypt(m):
    A = V.random_element()
    b = A * S + m
    return A, b
 
 
class Challenge:
    def __init__(self):
        self.before_input = "Would you like to encrypt your own message, or see an encryption of a character in the flag?\n"
 
    def challenge(self, your_input):
        if 'option' not in your_input:
            return {'error': 'You must specify an option'}
 
        if your_input['option'] == 'get_flag':
            if "index" not in your_input:
                return {"error": "You must provide an index"}
                self.exit = True
 
            index = int(your_input["index"])
            if index < 0 or index >= len(FLAG) :
                return {"error": f"index must be between 0 and {len(FLAG) - 1}"}
                self.exit = True
 
            A, b = encrypt(FLAG[index])
            return {"A": str(list(A)), "b": str(int(b))}
 
        elif your_input['option'] == 'encrypt':
            if "message" not in your_input:
                return {"error": "You must provide a message"}
                self.exit = True
 
            message = int(your_input["message"])
            if message < 0 or message >= p:
                return {"error": f"message must be between 0 and {p - 1}"}
                self.exit = True
 
            A, b = encrypt(message)
            return {"A": str(list(A)), "b": str(int(b))}
 
        return {'error': 'Unknown action'}
 
 
import builtins; builtins.Challenge = Challenge # hack to enable challenge to be run locally, see https://cryptohack.org/faq/#listener
listener.start_server(port=13411)

Đối với bài này thì hàm encrypt không cộng thêm errors vào

def encrypt(m):
    A = V.random_element()
    b = A * S + m
    return A, b

Cho nên ta có 2 cách để lấy lại được secret key $S$ và giải flag. Cách đầu tiên là từ việc ta biết trước prefix của flag là crypto{ cho nên ta có thể gọi get_flag(idx) để lấy $b=A\cdot S-flag[i]$
Cách thứ hai là gọi server trả về ciphertext của $m=0$ là được.
Solve script:

from pwn import * 
from sage.all import * 
import json 
context.log_level = 'debug'
import ast 
r = remote("socket.cryptohack.org",13411)
n = 64
p = 257
q = 0x10001
 
print(r.recvline())
 
def send_json(io, obj):
    io.sendline(json.dumps(obj).encode())
def recv_json(io):
    return json.loads(io.recvline().decode())
V = VectorSpace(GF(q), n)
# S = V.random_element()
# def encrypt(m):
#     A = V.random_element()
#     b = A * S + m
#     return A, b
 
def get_flag(idx):
    send_json(r,{"option":"get_flag","index":str(idx)})
    data = recv_json(r)
    return data["A"], data["b"]
rows = []
rhs = []
for _ in range(n):
    A, b = get_flag(0)
    A, b= ast.literal_eval(A), int(b) - 99 
    A_, b_ = vector(GF(q),A), GF(q)(b) 
    rows.append(A_)
    rhs.append(b_)
F = GF(q)
A_mat = Matrix(F, rows)      # n x n
b_vec = vector(F, rhs) 
S = A_mat.solve_right(b_vec)
print(S)
 
def decrypt(A_list,b_int,S):
    F = GF(q)
    A = vector(F,A_list)
    b = F(b_int)
    v = int(b-A*S) % q 
    assert 0<=v<=256
    return v 
FLAG = b"crypto{????????????????????????}"
m = len(FLAG)
flag = b""
for _ in range(m):
    A, b = get_flag(_)
    char = decrypt(A,b,S)
    flag+=chr(char).encode()
print(flag)
# crypto{linear_algebra_is_useful}  

Bounded Noise

import random
import json
 
FLAG = b"crypto{?????????????????????????????????????????}"
 
 
def keygen(secret, q, erange=range(2)):
    n, m = len(secret), len(secret) ** 2
    A = Matrix(GF(q), m, n, lambda i, j: randint(0, q - 1))
    e = vector(random.choices(erange, k=m), GF(q))
    b = (A * secret) + e
    return A, b, e
 
 
flag_int = int.from_bytes(FLAG, "big")
q = 0x10001
secret_key = []
while flag_int:
    secret_key.append(flag_int % q)
    flag_int //= q
 
secret_key = vector(GF(q), secret_key)
A, b, e = keygen(secret_key, q)
 
with open("output.txt", "w") as f:
    json.dump({"A": str(list(A)), "b": str(b)}, f)

Bài này có 2 cách giải.
Cách đầu tiên là dùng Arora–Ge attack và cách thứ hai là dùng LLL. Ở đây mình sẽ trình bày cách sử dụng LLL để thuận tiện làm cho các bài sau.
Có 2 attack chính đối với các hệ mật dựa trên LWE đó là Primal attack và Dual attack.

Đối với bài này thì $b=As+e$ nhưng $e$ khá nhỏ, do nó chỉ có 2 giá trị là $0$ hoặc $1$. Secret key của ta là các hệ số của flag trong cơ số $q$.

Ta có thể xem xét các quan hệ sau

$$\begin{array}{c}\{\begin{array}{ll}{a}_{1}s+e_1=b_1& \mathrm{mod}q\\ a_{2}s+e_2=b_2& \mathrm{mod}q\\ ...& \\ a_{m}s+e_m=b_m& \mathrm{mod}q\end{array}\end{array}$$

Bỏ đi modulo $q$ bằng cách thêm vào các hệ số $k_1,...,k_m$ như sau

$$\begin{array}{c}\{\begin{array}{ll}{a}_{1}s+k_{1}q=b_1-e_1& \\ ...& \\ a_{m}s+k_{m}q=b_m-e_m& \end{array}\end{array}$$

Ta xét một lattice như sau:

$$\begin{array}{c}(s_1,s_2,...,s_n,k_1,k_2,...,k_m)\left(\begin{array}{ccccc}{a}_{11}& a_{21}& & & a_{m1}\\ a_{12}& a_{22}& & & a_{m2}\\ ⋮& ⋮& & & ⋮\\ a_{1n}& a_{2n}& & & a_{mn}\\ q& & & & \\ & 0& & & \\ & & 0& & \\ & & & \ddots & \\ & & & & q\end{array}\right)=(b_1-e_1,b_2-e_2,...,b_m-e_m)=b^{\prime }\approx b\end{array}$$

Với tổ hợp tuyến tính $(s_1,s_2,...,s_n,k_1,...,k_m)$ thì ta kì vọng sẽ sinh ra một vector ngắn trong lưới đó là $(b_1-e_1,...,b_m-e_m)$. Ta sẽ giải bài toán CVP với target vector là $b$. Sau khi có $b^{\prime }$ thì ta sẽ giải tìm lại $s$ thỏa mãn $As=b^{\prime }$.

Ý tưởng là như vậy còn bây giờ mình sẽ thử code xem sao.

from sage.all import * 
import ast 
import json 
from sage.modules.free_module_integer import IntegerLattice
 
from pwn import *
context.log_level = "debug"
with open("/home/duccorp/CTF/CryptoHack/lattice/lwe/output.txt") as f:
    data = json.load(f)
FLAG = b"crypto{?????????????????????????????????????????}"
def flatter(M):
    import re
    from subprocess import check_output
    # compile https://github.com/keeganryan/flatter and put it in $PATH
    z = "[[" + "]\n[".join(" ".join(map(str, row)) for row in M) + "]]"
    ret = check_output(["flatter"], input=z.encode())
    return matrix(M.nrows(), M.ncols(), list(map(int, re.findall(b"-?\\d+", ret))))
 
def Babai_closest_vector(B, target):
    # Babai's Nearest Plane algorithm
    M = B.LLL()
    G = M.gram_schmidt()[0]
    small = target
    for _ in range(1):
        for i in reversed(range(M.nrows())):
            c = ((small * G[i]) / (G[i] * G[i])).round()
            small -= M[i] * c
    return target - small
 
A = ast.literal_eval(data["A"])
b = ast.literal_eval(data["b"])
q = 0x10001
print(A,"\n")
print(b,"\n")
F = GF(q)
A_mat = Matrix(ZZ,A)
b_vec = vector(ZZ, b)
m = A_mat.nrows()
n = A_mat.ncols()
print(m)
print(n)
B = block_matrix([[A_mat,q*identity_matrix(ZZ,m)]])
B_ = B.transpose()
print(f"Doing LLL")
L = IntegerLattice(B_, lll_reduce=False)
print(f"Done LLL")
B_reduction = L.BKZ(block_size = 20)
print(f"Done BKZ")
res = Babai_closest_vector(B_reduction, b_vec)
print("Closest Vector: {}".format(res))

Và nó chạy rất lâu =))). Lí do là vì ma trận của ta có kích thước khá là khủng $625\times 25$
Một cách khác đó là xài Primal Attack như sau:

from sage.all import * 
import random 
import json 
import ast 
def flatter(M):
    import re
    from subprocess import check_output
    # compile https://github.com/keeganryan/flatter and put it in $PATH
    z = "[[" + "]\n[".join(" ".join(map(str, row)) for row in M) + "]]"
    ret = check_output(["flatter"], input=z.encode())
    return matrix(M.nrows(), M.ncols(), list(map(int, re.findall(b"-?\\d+", ret))))
def primal_attack(A,b,fll = False):
    m = A.nrows()
    n = A.ncols()
    A_ = matrix(ZZ, A.T.rref().submatrix(0,n,n,m-n))
    print(f"building first block ok")
    b_zz = [int(x) for x in b]
    I_n = identity_matrix(ZZ,n)
    qAry = q*identity_matrix(ZZ,m-n)
    zero_mn_n = zero_matrix(ZZ, m-n, n)    
    zero_n_1  = zero_matrix(ZZ, n, 1)  
    zero_mn_1 = zero_matrix(ZZ, m-n, 1)    
    c1 = matrix(ZZ, 1, n,    b_zz[:n])    
    c2 = matrix(ZZ, 1, m-n,  b_zz[n:]) 
    t  = matrix(ZZ, 1, 1, [1])
    B = block_matrix([
    [I_n,        A_,   zero_n_1],
    [zero_mn_n,  qAry,   zero_mn_1],
    [c1,c2,t]
])
    print(f"done building block")
    if fll == True:
        L = flatter(B)
    else:
        L = B.LLL()
    print(f"done LLL")
    return L 
q = 0x10001
F = GF(q)
with open("/home/duccorp/CTF/CryptoHack/lattice/lwe/output.txt") as f:
    data = json.load(f)
A = ast.literal_eval(data["A"])
b = ast.literal_eval(data["b"])
A_mat = Matrix(GF(q), A)
b_vec = vector(GF(q), b)
 
# l = primal_attack(A_mat,b_vec)
# print(l)
# errors = []
# for row in l:
#     e_cand = row[:-1]
#     norm = e_cand.norm()
#     if norm == 0:
#         continue 
#     if all(0<=abs(x)<=3 for x in e_cand):
#         errors.append(e_cand)
# print(errors)
e = vector((0, 1, 1, 0, 1, 1, 1, 1, 1, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 1, 1, 0, 0, 1, 1, 1, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 1, 1, 0, 1, 1, 1, 0, 1, 0, 0, 0, 1, 1, 0, 0, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 1, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 0, 0, 0, 1, 0, 1, 0, 0, 1, 0, 0, 1, 1, 1, 1, 1, 0, 0, 0, 1, 0, 0, 1, 1, 0, 1, 0, 1, 0, 0, 1, 1, 1, 1, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 0, 1, 1, 1, 1, 1, 1, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 1, 1, 1, 1, 0, 1, 0, 1, 0, 1, 1, 0, 1, 1, 0, 0, 0, 1, 1, 1, 1, 0, 1, 0, 1, 0, 1, 0, 1, 1, 1, 1, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 0, 1, 0, 0, 1, 1, 1, 1, 0, 0, 1, 1, 0, 1, 0, 1, 0, 0, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 1, 1, 1, 1, 0, 1, 0, 0, 0, 1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 0, 1, 1, 1, 1, 0, 1, 0, 0, 0, 0, 1, 1, 0, 1, 1, 0, 0, 0, 0, 1, 1, 0, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 1, 1, 0, 0, 0, 0, 1, 0, 0, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 1, 1, 1, 0, 0, 0, 1, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 1, 0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 1, 1, 1, 1, 1, 1, 0, 0, 1, 0, 0, 0, 0, 1, 0, 1, 0, 1, 0, 1, 0, 0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 0, 0, 1, 0, 0, 0, 1, 1, 0, 1, 1, 1, 0, 0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 1, 0, 1, 0, 0, 0, 1, 1, 0, 1, 0, 1, 0, 0, 1, 1, 0, 0, 1, 1, 0, 1, 1, 1, 0, 0, 0, 0, 0, 1, 1, 0, 1, 0, 0, 1, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 0, 1, 0, 1, 1, 0, 0, 0, 0, 1, 1, 0, 0, 1, 0, 1, 0, 0, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 1, 0, 0, 1, 1, 1, 0, 0, 0, 1, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 1, 0, 0, 1, 1, 0, 0, 0, 1, 0, 1, 1, 1, 0, 1, 0, 1, 1, 1, 0, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1, 1, 0, 0, 1, 0, 0, 0, 1, 1, 0, 1, 1, 1, 0, 1, 1, 0, 0, 0, 0, 0, 1, 1),GF(q))
 
secret = matrix(F, A_mat).solve_right(vector(F, b_vec) - vector(F, e))
print(secret)
 
# (8590, 6465, 17312, 58487, 33027, 37469, 18625, 24033, 57830, 22541, 59008, 51941, 8396, 59708, 60960, 30756, 329, 52261, 21735, 5440, 61891, 54608, 37567, 26919, 99)
from Crypto.Util.number import long_to_bytes
flag = 0
for rem in secret[::-1]:
    flag *= q 
    flag += int(rem)
print(long_to_bytes(flag))

Do bài đã quá dài rồi nên mình xin dừng ở đây. Những attacks còn lại mình sẽ viết trong bài tiếp theo.
Lattice Methods - Part 2

Tài liệu tham khảo

[1] Abstract Algebra: Theory and Applications ,Thomas W. Judson, Stephen F. Austin, State University, August 11, 2012
[2] Predicting Lattice Reduction, Nicolas Gama and Phong Q.Nguyen
[3] NGHIÊN CỨU MỘT SỐ HỆ MẬT LATTICE TRONG HỌ MÃ HÓA ĐỒNG CẤU ĐẦY ĐỦ, Khuất Thanh Sơn, Nguyễn Trường Thắng, Lê Phê Đô, Bùi Trọng A Đam
[4] Giáo trình đại số tuyến tính - Ngô Việt Trung, Bộ sách cao học, Viện toán học.
[5] Determinants and Volumes
[6] https://github.com/Giapppp/Lattice-Based-Cryptography
[7] A Gentle Tutorial for Lattice-Based Cryptanalysis, https://eprint.iacr.org/2023/032.pdf
[8] A Course in Computational Algebraic Number Theory, Henri Cohen, Springer
[9] https://magicfrank00.github.io/writeups/posts/lll-to-solve-linear-equations/
[10] https://ur4ndom.dev/static/files/latticetraining/practical_lattice_reductions.pdf
[11] Algorithms for the Approximate Common Divisor Problem
[12] The Learning with Errors Problem - Oded Regev
[13] Attacks on LWE
[14] A Complete Analysis of the BKZ Lattice Reduction Algorithm
[15] A Brief Introduction to Techniques for Solving Lattice-based Quantum-Safe Schemes
[16] Lattice for beginners