Lattice Methods - Part 2

Truncated LCG

Cơ bản về LCG

Ở phần này ta sẽ tập trung vào khai thác một dạng PRNG đơn giản đó chính là Linear congruential generator.
Generator sẽ có dạng một biểu thức truy hồi tuyến tính (đây cũng sẽ là dạng biểu thức mà ta sẽ nghiên cứu trong phần mở rộng sau này):

$$X_{n+1}=(a{X}_n+c)\mathrm{mod}m$$

Dãy các giá trị sẽ được kí hiệu là $X$, trong đó

• $m$ được gọi là modulus của dãy
• $a,0<a<m$ là multiplier
• $c,0\le c<m$ là increment
• $X_0,0\le X_0<m$ được gọi là seed của dãy
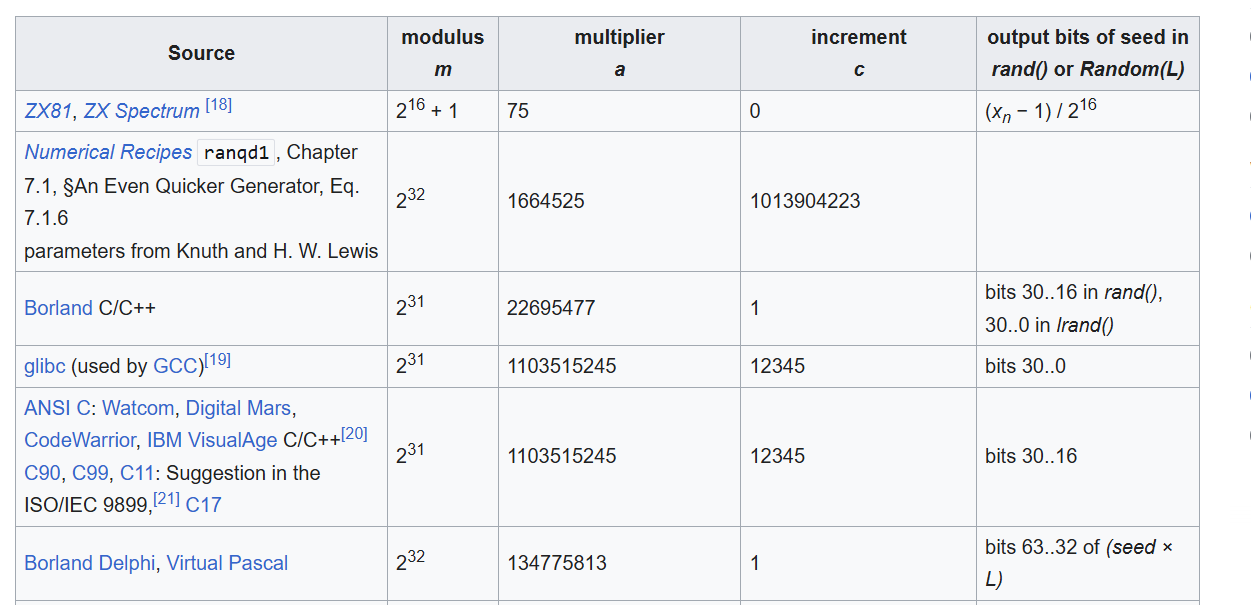
  Ví dụ một số bộ tham số $(m,a,c)$ cho LCG như sau: https://en.wikipedia.org/wiki/Linear_congruential_generator
  

class LCG:
    m = 2**31
    a = 1103515245
    c = 12345
    def __init__(self,seed):
        self.seed = seed
    def next(self):
        self.seed = (self.seed*self.a + self.c) % self.m 
        return self.seed 
 
if __name__ == "__main__":
    lcg = LCG(42)
    for _ in range(10):
        print(lcg.next())
 

Ta có thể viết lại từng số dạng trong dãy LCG dưới dạng tổng quát như sau:

$$\begin{array}{l}{X}_1=a{X}_0+c\mathrm{mod}m\\ X_2=a{X}_1+c=a(a{X}_0+c)+c=a^2{X}_0+c(a+1)=a^2{X}_0+\frac{a^2-1}{a-1}c\mathrm{mod}m\\ X_3=a{X}_2+c=a(a^2{X}_0+c(a+1))+c=a^3{X}_0+c(a^2+a+1)\mathrm{mod}m\\ =a^3{X}_0+\frac{a^3-1}{a-1}c\mathrm{mod}m\end{array}$$

Như vậy ta có thể biểu diễn, trong trường hợp $\gcd (a-1,m)=1$ , dãy LCG dưới dạng

$$X_j=a^j{X}_0+\frac{a^j-1}{a-1}c\mathrm{mod}m$$

Còn nếu không thì ta sẽ biểu diễn như sau:

$$X_j=a^j{X}_0+(a^{j-1}+a^{j-2}+...+1)c\mathrm{mod}m$$

Do LCG được lấy theo modulo $m$ cho nên theo nguyên lí Dirichlet thì dãy sẽ lặp lại các số hạng kể từ một lúc nào đó. Tức là tồn tại hai chỉ số $i,j$ sao cho $X_i=X_j,i\ne j$. Như vậy để LCG trở nên “an toàn” hơn thì ta cần chọn $m$ đủ lớn và các tham số $a,c$ sao cho chu kì của dãy là đủ dài.
Về việc này, mọi người có thể đọc qua định lý Hull-Dobell tại đây.

So, how to break it?

Sẽ có 3 trường hợp có thể xảy ra

Trường hợp 1. Ta chỉ biết thông tin về $(a,m)$, khôi phục $c$ và seed.
Đối với trường hợp này ta chỉ cần 2 output liên tiếp là sẽ khôi phục được $c$. Giả sử ta có $(X_j,X_{j+1})$ thì ta tính lại được $c$ bằng cách lấy:

$$X_{j+1}-a{X}_j=c\mathrm{mod}m$$

Sau khi có được $c$ và một output $X_j$ rồi thì ta có thể thử recover lại seed từ công thức tổng quát của dãy LCG như trên:

$$\begin{array}{l}{X}_j=a^j{X}_0+c\sum _{i=0}^{j-1}{a}^i\mathrm{mod}m\\ \to X_j-c\sum _{i=0}^{j-1}{a}^i=a^j{X}_0\mathrm{mod}m\\ \to a^{-j}(X_j-c\sum _{i=0}^{j-1}{a}^i)=X_0\mathrm{mod}m\end{array}$$

Test:

import random 
class LCG:
    m = 2**31
    a = 1103515245
    c = 12345
    def __init__(self,seed):
        self.seed = seed
    def next(self):
        self.seed = (self.seed*self.a + self.c) % self.m 
        return self.seed 
 
if __name__ == "__main__":
    seed = random.randrange(2**31)
    a = 1103515245
    print(f"orignial seed: {seed}")
    lcg = LCG(seed)
    for _ in range(10):
        print(f"x{_+1} : {lcg.next()}")
    x11 = lcg.next()
    x12 = lcg.next()
    c = (x12 - a*x11) % 2**31
    print(f"c : {c}")
    s  = sum([a**i for i in range(11)])
    seed_rec = (pow(a,-11,2**31)*(x11-c*s)) % 2**31
    print(f"reconstructed seed : {seed_rec}")

Trường hợp 2. Ta chỉ biết modulus $m$. Cần tìm lại $a,c$.
Việc tìm lại $c$ cũng tương tự như trên, chỉ cần biết 2 output liên tiếp thì ta sẽ tìm lại được $c$.
Chẳng hạn ta có

$$X_{j+1}=a{X}_j+c\mathrm{mod}m$$

Thì ta có thể tính lại $a$ bằng cách lấy:

$$(X_{j+1}-c)X_j^{-1}=a\mathrm{mod}m$$

Khi và chỉ khi $\gcd (X_j,m)=1$.
Nếu như ta không có được $(X_j,m)=1$ thì ta cần thêm ít nhất 1 output nữa $X_{j+2}$ để có thể recover được $a$.
Cụ thể

$$X_{j+2}=a{X}_{j+1}+c$$

Ta có

$$X_{j+2}-X_{j+1}=a(X_{j+1}-X_j)$$

Cho nên

$$a=\frac{X_{j+2}-X_{j+1}}{X_{j+1}-X_j}\mathrm{mod}m$$

Nếu như LCG của ta thỏa mãn các điều kiện của định lí Hull-Dober bên trên thì khi đó sẽ tồn tại nghịch đảo modulo $m$ của $X_{j+1}-X_j$.
Test:

import random 
class LCG:
    m = 2**31
    a = 1103515245
    c = 12345
    def __init__(self,seed):
        self.seed = seed
    def next(self):
        self.seed = (self.seed*self.a + self.c) % self.m 
        return self.seed 
 
if __name__ == "__main__":
    seed = random.randrange(2**31)
    a = 1103515245
    print(f"orignial seed: {seed}")
    lcg = LCG(seed)
    for _ in range(10):
        print(f"x{_+1} : {lcg.next()}")
    x11 = lcg.next()
    x12 = lcg.next()
    x13 = lcg.next()
    c = (x12 - a*x11) % 2**31
    a = ((x13-x12)*pow(x12-x11,-1,2**31)) % 2**31
    print(a)

Trường hợp 3. Trường hợp cuối cùng là khi ta không biết bất cứ thông tin gì về $a,c,m$.
Để giải trường hợp này thì ta cần ít nhất 5 output liên tiếp của dãy LCG.
Ta xét 5 output đó lần lượt là $X_i,X_{i+1},X_{i+2},X_{i+3},X_{i+4}$.
Đặt $d_j=X_j-X_{j-1}$ thì ta có được

$$\begin{array}{l}{d}_{i+2}=a{d}_{i+1}\mathrm{mod}m\\ d_{i+3}=a{d}_{i+2}\mathrm{mod}m\end{array}$$

Ta sẽ tiến hành nhân chéo lên như sau:

$$\begin{array}{l}{d}_{i+2}{d}_{i+2}a\equiv a{d}_{i+1}{d}_{i+3}\mathrm{mod}m\\ \to a(d_{i+2}^2-d_{i+3}{d}_{i+1})\equiv 0\mathrm{mod}m\end{array}$$

Do $(a,m)=1$ nên ta có thể suy ra $d_{i+2}^2-d_{i+3}{d}_{i+1}\equiv 0\mathrm{mod}m$. Làm tương tự ta cũng có được

$$\begin{array}{l}{d}_{i+4}=a{d}_{i+3}\mathrm{mod}m\\ \to d_{i+3}^2-d_{i+4}{d}_{i+2}\equiv 0\mathrm{mod}m\end{array}$$

Sau đó ta lấy ước chung của 2 biểu thức trên và khôi phục lại $m$. Sau khi có $m$ rồi thì ta làm như 2 trường hợp trên để lấy lại $a,c$.
Test:

import random 
from sage.all import gcd 
from factordb.factordb import FactorDB
class LCG:
    m = 2**31
    a = 1103515245
    c = 12345
    def __init__(self,seed):
        self.seed = seed
    def next(self):
        self.seed = (self.seed*self.a + self.c) % self.m 
        return self.seed 
 
if __name__ == "__main__":
    seed = random.randrange(2**31)
    a = 1103515245
    print(f"orignial seed: {seed}")
    print(f"modulus = {LCG.m}")
    lcg = LCG(seed)
    for _ in range(10):
        print(f"x{_+1} : {lcg.next()}")
    x = [lcg.next() for _ in range(5)]
    d = [x[i+1]-x[i] for i in range(4)]
    u = d[1]**2-d[2]*d[0]
    v = d[2]**2 - d[3]*d[1]
    res = int(gcd(u,v))
    print(res)
    f = FactorDB(res)
    f.connect()
    lst = f.get_factor_from_api()
    print(lst)

Bài tập ví dụ: RSA vs RNG / CryptoHack
Source code của bài:

from Crypto.Util.number import *
import json
 
MOD = 2**512
A = 2287734286973265697461282233387562018856392913150345266314910637176078653625724467256102550998312362508228015051719939419898647553300561119192412962471189
B = 4179258870716283142348328372614541634061596292364078137966699610370755625435095397634562220121158928642693078147104418972353427207082297056885055545010537
 
FLAG = b'crypto{???????????????????????????}'
 
class PRNG:
    def __init__(self, seed):
        self.state = (seed % MOD)
 
    def get_num(self):
        self.state = (A * self.state + B) % MOD
        return self.state
 
    def get_prime(self):
        p = self.get_num()
        while not isPrime(p):
            p = self.get_num()
        return p
 
seed = getRandomRange(1, MOD)
rng = PRNG(seed)
 
P = rng.get_prime()
Q = rng.get_prime()
 
N = P * Q
E = 0x10001
pt = bytes_to_long(FLAG)
ct = long_to_bytes(pow(pt, E, N))
 
json.dump({{"N": 95397281288258216755316271056659083720936495881607543513157781967036077217126208404659771258947379945753682123292571745366296203141706097270264349094699269750027004474368460080047355551701945683982169993697848309121093922048644700959026693232147815437610773496512273648666620162998099244184694543039944346061, "E": 65537, "ciphertext": "04fee34327a820a5fb72e71b8b1b789d22085630b1b5747f38f791c55573571d22e454bfebe0180631cbab9075efa80796edb11540404c58f481f03d12bb5f3655616df95fb7a005904785b86451d870722cc6a0ff8d622d5cb1bce15d28fee0a72ba67ba95567dc5062dfc2ac40fe76bc56c311b1c3335115e9b6ecf6282cca"}
    'N': N,{"N": 95397281288258216755316271056659083720936495881607543513157781967036077217126208404659771258947379945753682123292571745366296203141706097270264349094699269750027004474368460080047355551701945683982169993697848309121093922048644700959026693232147815437610773496512273648666620162998099244184694543039944346061, "E": 65537, "ciphertext": "04fee34327a820a5fb72e71b8b1b789d22085630b1b5747f38f791c55573571d22e454bfebe0180631cbab9075efa80796edb11540404c58f481f03d12bb5f3655616df95fb7a005904785b86451d870722cc6a0ff8d622d5cb1bce15d28fee0a72ba67ba95567dc5062dfc2ac40fe76bc56c311b1c3335115e9b6ecf6282cca"}
    'E': E,
    'ciphertext': ct.hex()
}, open('flag.enc', 'w'))

Và một file json data chứa các tham số $N$, $E$ và ciphertext

{"N": 95397281288258216755316271056659083720936495881607543513157781967036077217126208404659771258947379945753682123292571745366296203141706097270264349094699269750027004474368460080047355551701945683982169993697848309121093922048644700959026693232147815437610773496512273648666620162998099244184694543039944346061, "E": 65537, "ciphertext": "04fee34327a820a5fb72e71b8b1b789d22085630b1b5747f38f791c55573571d22e454bfebe0180631cbab9075efa80796edb11540404c58f481f03d12bb5f3655616df95fb7a005904785b86451d870722cc6a0ff8d622d5cb1bce15d28fee0a72ba67ba95567dc5062dfc2ac40fe76bc56c311b1c3335115e9b6ecf6282cca"}

Bài cho ta một modulo và cặp số $A,B$. class PRNG sẽ lấy đầu vào là một seed.

Ta gọi state ban đầu là $x$ chẳng hạn thì $state=seed\mathrm{mod}MOD$.

Ở mỗi bước, khi ta gọi hàm get_num nó sẽ tính $(Ax+B)\mathrm{mod}{2}^{512}$ còn khi gọi get_prime thì nó sẽ lấy $p=(Ax+B)\mathrm{mod}{2}^{512}$ liên tục cho tới khi $p$ là số nguyên tố.
Mấu chốt của bài này là hai số nguyên tố $p,q$ được sinh ra từ cùng 1 seed và ta phải tìm cách khôi phục lại 2 số này để giải RSA.

Đầu tiên ta thử viết lại $p,q$ theo $A,B,x$.

Giả sử thực hiện $i$ lần. Thì khi đó $p=A{x}_i+B$. Giả sử $i⩾3$ chẳng hạn, mình muốn tìm một công thức gọn hơn cho $p$ theo $A,x,B$, trong đó $x_1=x=seed$

$$\begin{array}{c}{x}_i=A{x}_{i-1}+B\\ ⟹p=A{x}_i+B=A(A{x}_{i-1}+B)+B=A^2{x}_{i-1}+AB+B\\ =A^2(A{x}_{i-2}+B)+AB+B\\ =A^3{x}_{i-2}+A^{2}B+AB+B=B\left(A^2+A+1\right)+A^3{x}_{i-2}\\ =....=A^{i}x+B\sum _{j=0}^{i-1}{A}^j=A^{i}x+B\frac{A^i-1}{A-1}\end{array}$$

Như vậy mình có được

$$\begin{array}{c}p=A^{i}x+B\frac{A^i-1}{A-1}\mathrm{mod}{2}^{512}\end{array}$$

Tương tự, nếu như ta thực hiện $j$ lần để get_num() tạo ra số $q$ thì khi đó

$$\begin{array}{c}q=A^{j}x+B\frac{A^j-1}{A-1}\mathrm{mod}{2}^{512}\end{array}$$

Ở đây ta gọi lấy $p$ trước rồi mới lấy $q$ tức là trạng thái state khi ta gọi $q$ sẽ là chuyển tiếp từ trạng thái của $p$ cho nên ta có $j=i+t$ với $t$ là một số nào đó mà ta không rõ.

Vậy thì

$$\begin{array}{c}p=A^{i}x+B\frac{A^i-1}{A-1}\mathrm{mod}{2}^{512}\\ q=A^{i+t}x+B\frac{A^{i+t}-1}{A-1}\mathrm{mod}{2}^{512}\end{array}$$

Bây giờ ta có

$$\begin{array}{c}q=A^{i+t}x+B\left(A^{i+t-1}+...+1\right)\mathrm{mod}{2}^{512}\\ p=A^{i}x+B\left(A^{i-1}+...+1\right)\mathrm{mod}{2}^{512}\end{array}$$

Xét

$$\begin{array}{c}{A}^t\left(\underset{=p}{\underbrace{A^{i}x+B\left(A^{i-1}+...+1\right)}}\right)+B\left(A^{t-1}+...+1\right)\mathrm{mod}{2}^{512}\\ =A^{t+i}x+B\left(A^{t+i-1}+...+A^t\right)+B\left(A^{t-1}+...+1\right)\mathrm{mod}{2}^{512}\\ =A^{t+i}x+B\left(A^{t+i-1}+...+A^t+A^{t-1}+...+1\right)=q\\ ⟹q=A^{t}p+B\left(A^{t-1}+...+1\right)\mathrm{mod}{2}^{512}\\ ⟹pq-N=A^t{p}^2+B\left(A^{t-1}+...+1\right)p-N=0\mathrm{mod}{2}^{512}\end{array}$$

Ta có phương trình bậc 2 với các hệ số

$$\begin{array}{c}\{\begin{array}{ll}a=A^t& \\ b=B\left(A^{t-1}+...+1\right)=B{\sum }_{j=0}^{t-1}{A}^j& \\ c=-N& \end{array}\end{array}$$

Lưu ý ở bài này $A$ là số lẻ cho nên ta không thể lấy $(A-1{)}^{-1}$ được.

Giả sử ta muốn giải

$$\begin{array}{c}f(x)=a{x}^2+bx+c\\ ⟹\Delta =\sqrt{b^2-4ac}\\ ⟹r_{1,2}=\frac{-b\pm \sqrt{b^2-4ac}}{2a}\\ ⟹2r_{1,2}\equiv \left(-b\pm \sqrt{b^2-4ac}\right)a^{-1}\mathrm{mod}{2}^{512}\\ ⟹r_{1,2}=\frac{\left(-b\pm \sqrt{b^2-4ac}\right)a^{-1}}{2}\mathrm{mod}{2}^{511}\end{array}$$

Mấu chốt ở đây là reduce từ modulo $2^{512}$ về modulo $2^{511}$.

Ta không thể chia 2 trên modulo $2^{512}$ được, giả sử ta có một số $r$ chẳng hạn và ta biết $r⋮2$. Ta muốn tính $\frac{r}{2}\mathrm{mod}{2}^{512}$ thì ta cần làm sao?

Đầu tiên ta viết $r=k+t{2}^{512}$ thì khi đó $\frac{r}{2}=\frac{k}{2}+t{2}^{511}$. Ta lấy $r$ chia lấy phần nguyên cho 2 rồi sau đó tính modulo theo $2^{511}$ là ra được số dư, sau đó nếu muốn lift lên modulo $2^{512}$ lại thì ta cần cộng thêm $t{2}^{511}$ với $t\in \{0,1\}$ (vì các số trong bài lấy theo modulo $2^{512}$ nên không thể quá lớn được.)

from sage.all import *
from Crypto.Util.number import *
MOD = 2**512
A = 2287734286973265697461282233387562018856392913150345266314910637176078653625724467256102550998312362508228015051719939419898647553300561119192412962471189
B = 4179258870716283142348328372614541634061596292364078137966699610370755625435095397634562220121158928642693078147104418972353427207082297056885055545010537
 
class PRNG:
    def __init__(self, seed):
        self.state = (seed % MOD)
 
    def get_num(self):
        self.state = (A * self.state + B) % MOD
        return self.state
 
    def get_prime(self):
        p = self.get_num()
        while not isPrime(p):
            p = self.get_num()
        return p
 
N = 95397281288258216755316271056659083720936495881607543513157781967036077217126208404659771258947379945753682123292571745366296203141706097270264349094699269750027004474368460080047355551701945683982169993697848309121093922048644700959026693232147815437610773496512273648666620162998099244184694543039944346061
E = 65537
 
ciphertext = "04fee34327a820a5fb72e71b8b1b789d22085630b1b5747f38f791c55573571d22e454bfebe0180631cbab9075efa80796edb11540404c58f481f03d12bb5f3655616df95fb7a005904785b86451d870722cc6a0ff8d622d5cb1bce15d28fee0a72ba67ba95567dc5062dfc2ac40fe76bc56c311b1c3335115e9b6ecf6282cca"
ct=int(ciphertext,16)
 
assert gcd(N,A)==1
x=0
found = true
while found:
    x+=1
    print(x)
    a = pow(A,x,MOD)
    b = B * sum(pow(A,i,MOD) for i in range(x)) % MOD
    c = - N 
    try:
        det = int(Mod(b ** 2 - 4 * a * c, MOD).nth_root(2))
        rt1 = (-b + det) * pow(a,-1,MOD) % MOD
        rt2 = (-b - det) * pow(a,-1,MOD) % MOD
        for k in range(2):
            p = (rt1 % (MOD // 2)) // 2 + k * (MOD // 2)
            if N % p == 0:
                print(p)
                q=N//p
                phi=(p-1)*(q-1)
                d=pow(E,-1,phi)
                m=pow(ct,d,N)
                print(long_to_bytes(m))
                found = false
            else:
                print("failed")
        for k in range(2):
            p = (rt2 % (MOD // 2)) // 2 + k * (MOD // 2)
            if N % p == 0:
                print(p)
                q=N//p
                phi=(p-1)*(q-1)
                d=pow(E,-1,phi)
                m=pow(ct,d,N)
                print(long_to_bytes(m))
                found=false
            else:
                print("failed")
    except:
        print("failed")

Truncated LCG

Knuth’s truncated LCG

Xét một LCG như sau:

$$x_{i+1}=a{x}_i+b\mathrm{mod}m,0\le x_i\le m-1,i=0,1,..$$

Gọi $k$ là bit length của $m$. Xét

$$x_i=2^{k-s}{y}_i+z_i,0\le z_i<2^{k-s}$$

Trong đó $s$ là số lượng MSB bit được leak ra và ta được biết toàn bộ các giá trị $y_i$ này.
Bài toán đặt ra sẽ là: Biết $s$ MSB của $x_i$ là $y_i$. Yêu cầu tìm lại $(a,c,m,x_0)$.
Trước tiên ta giới thiệu 1 số tham số:

• $k$ là bit length của modulus $m$
• $s$ là số lượng MSB được biết
• $\alpha =s/k$
  Attacks gồm 2 bước chính.
  Bước 1. Dựng đa thức và LLL
  Xét danh sách $Y$ gồm các giá trị đầu vào là $y_i$. Ta sẽ chia $Y$ thành các block, mỗi block bao gồm $n+t$ vector. Bắt đầu từ $y_1$ tới $y_{n+t}$. Các tham số $n,t$ ta sẽ chọn sao cho

$$t>1/\alpha ,n\approx \sqrt{2\alpha tk}$$

Mỗi vector $V_i$ mà ta build sẽ có dạng

$$V_i=(y_{i+1}-y_i,y_{i+2}-y_{i+1},...,y_{i+t}-y_{i+t-1})$$

Tiếp theo ta sẽ tìm một vector $\lambda =({\lambda }_1,{\lambda }_2,...,{\lambda }_n)$ thỏa mãn

$$\sum _{i=1}^n{\lambda }_i{V}_i=0$$

Xét lattice sau:

$$\left(\begin{array}{ccccc}K{V}_1& 1& & & \\ K{V}_2& & 1& & \\ ⋮& & & \ddots & \\ K{V}_n& & & & 1\end{array}\right)$$

Ta có thể đảm bảo rằng tồn tại một vector $\lambda$ thỏa ràng buộc tuyến tính trên nếu như $|{\lambda }_i|\le B$ với mọi $i$ và $B$ thỏa

$$B=2^{t(\alpha k+\log n+1)/(n-t)}$$

Ta sẽ chọn $K$ thỏa mãn $K=\lceil \sqrt{n}{2}^{(n-1)/2}B\rceil$ và ta kì vọng rằng vector tìm được sẽ có chuẩn Euclid không vượt quá $K$ và thỏa phương trình trên.
Tiếp theo ta xét các vector $W_i$ có dạng:

$$W_i=(x_{i+1}-x_i,x_{i+2}-x_{i+1},...,x_{i+t}-x_{i+t-1})$$

Với các parameters được chọn như trên, sẽ có một trong số các vector $\lambda$ thỏa mãn

$$U=\sum _{i=1}^n{\lambda }_i{W}_i=0$$

Test:

import random 
import math 
from sage.all import *
from itertools import combinations
class LCG:
    m = 10734367385013619889
    a = 9807963723765715717
    b = 7226300108115682840
    def __init__(self,seed):
        self.seed = seed
    def next(self):
        self.seed = (self.seed*self.a + self.b) % self.m 
        return self.seed 
seed = 2877244225168654778
lcg = LCG(seed)
m = LCG.m 
a = LCG.a 
b = LCG.b
# print(m.bit_length())
# generate truncated xs 
xs = []
ys = []
zs = []
mod = 2**32
alpha = 1/2
k = 64
s = 32
for _ in range(17):
    x = lcg.next()
    xs.append(x)
    ys.append(x >> 32)
    zs.append(x % mod) 
assert all(y*(2**32)+z==x for x,y,z in zip(xs,ys,zs))
# print(ys) # được biết ys
t = 3
n = 14
Vs = []
for i in range(n):
    V = []
    for j in range(t):
        V.append(ys[i+j+1]-ys[i+j])
    Vs.append(V)
K = 356131
 
Ws = []
for i in range(n):
    W = [] 
    for j in range(t):
        W.append(xs[i+j+1]-xs[i+j])
    Ws.append(W)
 
Vs = [vector(ZZ, v) for v in Vs]   
B = matrix(ZZ, [K * v for v in Vs])  
I = identity_matrix(ZZ, n)
M = B.augment(I)
L = M.LLL()
Ws = [vector(ZZ, w) for w in Ws]
print(Ws)
for v in L:
    v_ = v[3:]
    s_  = 0 
    for i in range(len(Ws)):
        s_ += v_[i] * Ws[i]
    print(s_)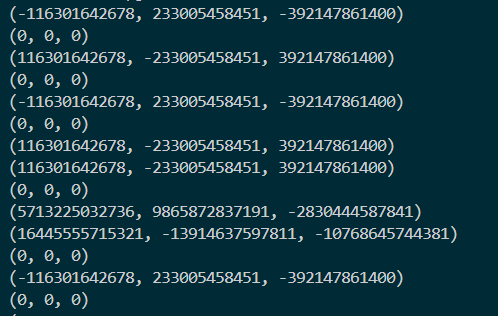

Tiếp theo ta có $x_j=a^j{x}_0+b\sum _{i=0}^{j-1}{a}^i\mathrm{mod}m$ . Cho nên

$$\begin{array}{c}{x}_{i+j+1}-x_{i+j}=a^{i+j+1}{x}_0+b\sum _{r=0}^{i+j}{a}^r-a^{i+j}{x}_0+b\sum _{r=0}^{i+j-1}{a}^r\\ =a^{i+j+1}{x}_0-a^{i+j}{x}_0+a^{i+j}\\ =a^j(x_{i+1}-x_i)\mathrm{mod}m\end{array}$$

Như vậy:
$W_i\equiv \left(a^{i-1}(x_2-x_1),a^i(x_2-x_1),...,a^{i+t-2}(x_2-x_1)\right)\mathrm{mod}m$. Nếu như $U=0$ thì khi đó xét đa thức

$$\begin{array}{c}f(X)=(x_2-x_1)\sum _{i=1}^n{\lambda }_i{X}^{i-1}\end{array}$$

thỏa mãn $f(a)\equiv 0\mathrm{mod}m$. Trong đa số các trường hợp thì $(x_2-x_1,m)=1$ nên ta có thể xét đa
thức

$$\begin{array}{c}P(X)=\sum _{i=1}^n{\lambda }_i{X}^{i-1}\end{array}$$

Các đa thức này có nghiệm chung là $a$ nên ta có thể dùng kết thức (resultant) để tính lại $m$.
Test:

R = PolynomialRing(ZZ,'x')
x = R.gen()
lamb = []
ps = []
for vec in L:
    P = sum(vec[3:][i]*x**i for i in range(n))
    print(P)
    print(P(a)%m) # for testing
    ps.append(P)
ms = []
# recover m 
for comb in combinations(ps,3):
    p0 = comb[0]
    p1 = comb[1]
    p2 = comb[2]
    m_ = math.gcd(p0.resultant(p1), p1.resultant(p2), p0.resultant(p2))
    print(m_)
    if (m_.bit_length() > 20):
        ms.append(m_)
print(set(ms))

Giải thích: Sau khi rút gọn LLL. thì ta sẽ lấy các vector trong L để build đa thức $P$. Sau đó sẽ tạo các tổ hợp gồm 3 đa thức và tính resultant của các cặp đa thức này.

Như vậy là ta đã có được một list các số có khả năng là modulus $m$.
Bước tiếp theo là recover lại $a$.

Ta biết rằng các đa thức này đều có nghiệm chung là $a$. Như vậy ta sẽ lấy GCD của chúng để thu được 1 đơn thức có nghiệm là $a$.

Bước tiếp theo ta cần recover lại $x_i,z_i,b$.

Ý tưởng 1. Mình thử đưa bài toán recover $z_i$ về bài HNP.
Nhắc lại bài toán HNP:
Bài toán HNP yêu cầu ta recover lại một số nguyên bí mật $\alpha \in [1,p-1]$ trong đó $p$ là số nguyên tố, từ $m$ cặp giá trị $\{(t_i,a_i){\}}_{i=1}^m$ thỏa mãn

$${\beta }_i-t_i\alpha +a_i=0(\mathrm{mod}p)$$

Đối với bài LCG của ta thì ta có:

$$x_i=2^{k-s}{y}_i+z_i,0\le z_i<2^{k-s}$$

Vì đa tìm được $a$ nên ta có thể thử viết lại dưới dạng sau:

$$x_{i+1}-x_i=2^{k-s}{y}_{i+1}-2^{k-s}{y}_i+z_{i+1}-z_i$$

Ta có $x_{i+1}=a{x}_i+b=a(2^{k-s}{y}_i+z_i)+b$ cho nên

$$\begin{array}{l}{2}^{k-s}{y}_{i+1}+z_{i+1}=a{2}^{k-s}{y}_i+a{z}_i+b(\mathrm{mod}m)\\ \to 2^{k-s}(y_{i+1}-a{y}_i)=a{z}_i-z_{i+1}+b(\mathrm{mod}m)\\ \to (a{z}_i-z_{i+1})-(-1)b+2^{k-s}(a{y}_i-y_{i+1})=0(\mathrm{mod}m)\end{array}$$

Ta đưa về dạng HNP với ${\beta }_i=a{z}_i-z_{i+1}<m$ và $t_i=-1,a_i=2^{k-s}(a{y}_i-y_{i+1})$
Nhưng rất tiếc là cách này không cho ta solutions vì các giá trị ${\beta }_i$ có bound quá lớn

Cụ thể

$$|{\beta }_i|=|a{z}_i-z_{i+1}|\le |a|\max (|z_i|,|z_{i+1}|)=B$$

Nhưng ta đang muốn $B\le m/2^k$ với $k$ được đánh giá như trên. $a$ gốc trong bài toán của ta gần như xấp xỉ $m$ nên cách này có vẻ không ổn lắm

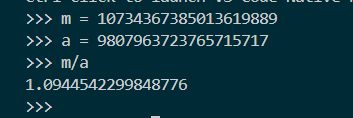
Vậy ta cần tìm một cách dựng ma trận khác hợp lí hơn.
Bây giờ ta có

$$\begin{array}{c}{x}_{i+1}\equiv a{x}_i+b(\mathrm{mod}m)\\ y_i=\lfloor \frac{x_i}{2^{k-s}}\rfloor ,0⩽y_i<2^s\end{array}$$

Từ công thức tổng quát của LCG ta có

$$\begin{array}{c}{x}_i=a^i{x}_0+\left(a^{i-1}+...+a+1\right)b(\mathrm{mod}m)\end{array}$$

Đặt các tham số

• $A_i^{(1)}=a^i\mathrm{mod}m$
• $A_i^{(2)}=a^{i-1}+...+a+1\mathrm{mod}m$
• ${\beta }_i=-X{y}_i$
  Thì khi đó từ $x_i=X{y}_i+{\epsilon }_i$ ta viết lại:

$$\begin{array}{c}{A}_i^{(1)}{x}_0+A_i^{(2)}b+{\epsilon }_i=-X{y}_i(\mathrm{mod}m)\end{array}$$

Với 2 unknown variables là $x_0,b$.

Tài liệu

• https://eprint.iacr.org/2022/1134.pdf
• https://eprint.iacr.org/2021/1204.pdf
• https://sci-hub.se/10.1007/11506157_5
• https://www.math.cmu.edu/~af1p/Texfiles/RECONTRUNC.pdf
• https://dunkirkturbo.github.io/2020/02/29/Lattice-Learning-1/
• https://link.springer.com/article/10.1007/s001459900042
• https://www.texmacs.org/joris/chinese-macis/chinese-macis.pdf
• https://cseweb.ucsd.edu/~mihir/papers/dss-lcg.pdf
• https://jia.je/ctf-writeups/misc/lcg.html
• https://math.stackexchange.com/questions/3597480/understanding-resultant

Shortest Integer solutions - SIS

Tài liệu

• https://eprint.iacr.org/2023/1125.pdf
• https://tover.xyz/p/G6k-Sage-Install/

Lattice’s sieving

• https://eprint.iacr.org/2025/304.pdf

Hermite Normal Form